Endocarp Development Study in Full Irrigated Olive Orchards and Impact on Fruit Features at Harvest
Abstract
1. Introduction
2. Results
2.1. Endocarp Hardening Model
2.2. Period I of Endocarp Development
2.3. Period II of Endocarp Development
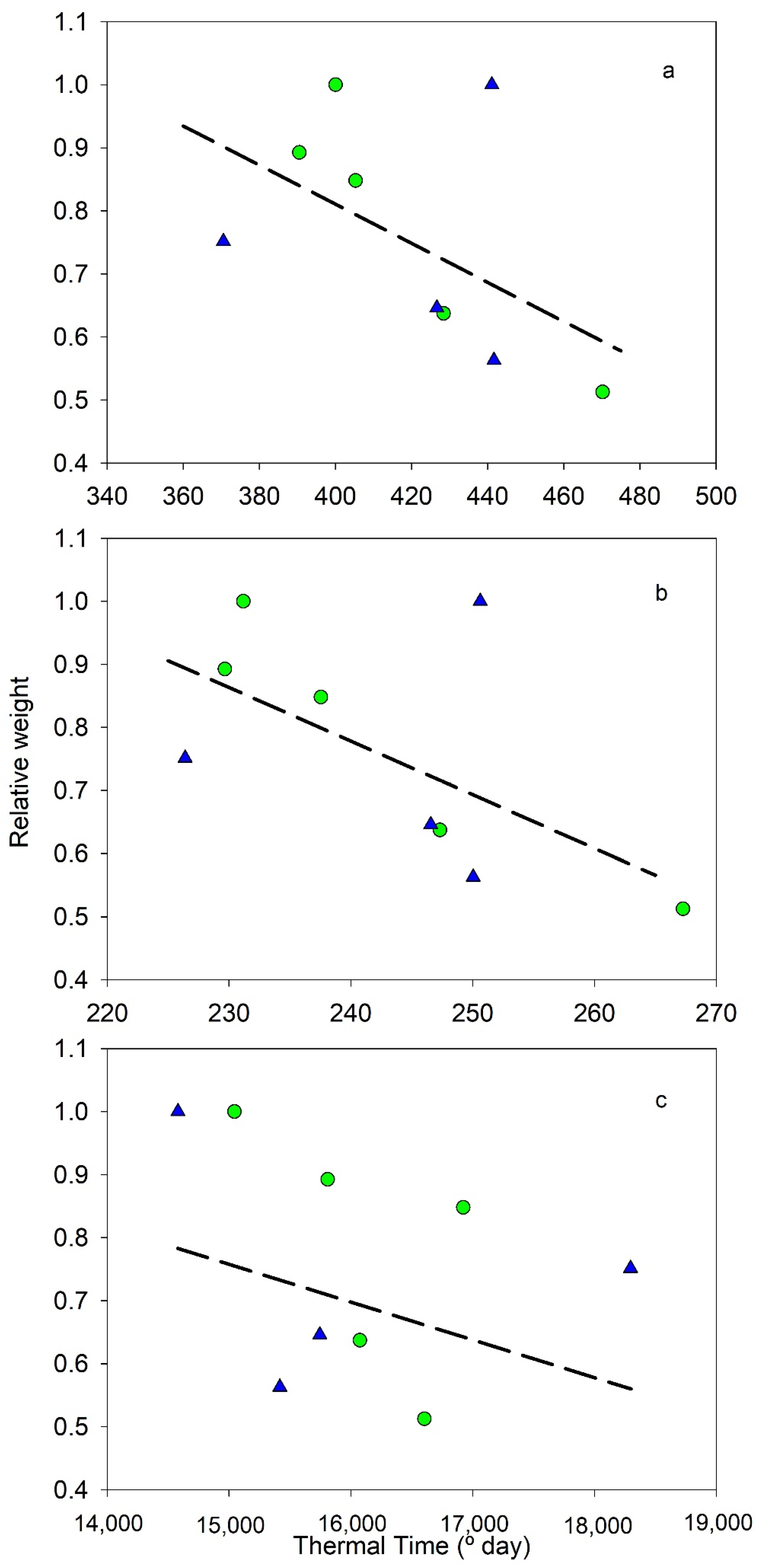
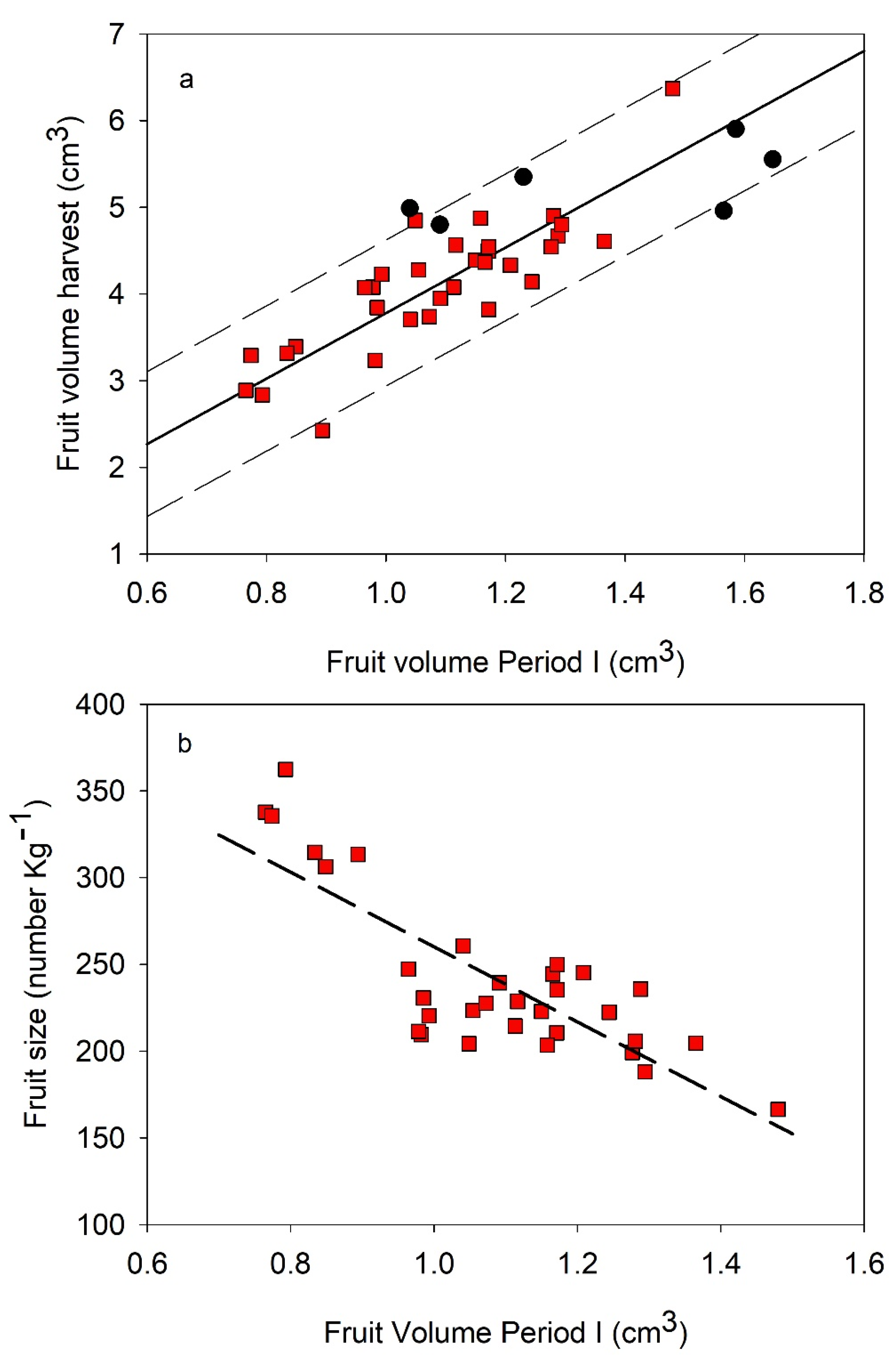
2.4. Prediction of Fruit Size
3. Discussion
3.1. Endocarp Development
3.2. Prediction of Fruit Size at Harvest
4. Materials and Methods
4.1. Sites Description
- Five seasons for cultivar Cornicabra at “Entresierra” experimental farm near Ciudad Real (39° N, 3°56′ W; altitude 640 m).
- Three seasons for cv Arbequina at the same location.
- One season for cv Arbequina at “El Morillo” farm near Seville (37.5° N, 5.7° W; 102 m altitude).
- Two seasons for cv Manzanilla de Sevilla at “La Hampa” experimental farm near Seville (37° 17′ N, 6° 3′ W, 30 m altitude).
4.2. Endocarp Development
4.3. Prediction of Fruit Size and Weight at Harvest
4.4. Data Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gucci, R.; Fereres, E.; Godhamer, D.A.; Steduto, P.; Hsiao, T.C.; Fereres, E.; Raes, D. (Eds.) Crop Yield Response to Water; FAO Irrigations and drainage paper 66; FAO: Rome, Italy, 2012; pp. 300–315. [Google Scholar]
- Goldhamer, D.A. Regulated deficit irrigation for California canning olives. Acta Hortic. 1999, 474, 369–372. [Google Scholar] [CrossRef]
- Rapoport, H.F.; Pérez-López, D.; Hammami, S.B.M.; Aguera, J.; Moriana, A. Fruit pit hardening: Physical measurements during olive growth. Ann. Appl. Biol. 2013, 163, 200–208. [Google Scholar] [CrossRef]
- Fernandez-Escobar, R.; Benlloch, M.; Navarro, C.; Martin, G.C. The time of floral induction in the olive. J. Amer. Soc. Hort. Sci. 1992, 117, 304–307. [Google Scholar] [CrossRef]
- Gomez del Campo, M.; Perez-Exposito, M.A.; Hammami, S.B.M.; Centeno, A.; Rapoporrt, H.F. Effect of varied summer deficit irrigation on components of olive fruit growth and development. Agric. Water Manag. 2014, 137, 84–91. [Google Scholar] [CrossRef]
- Gucci, R.; Caruso, G.; Gennai, C.; Esposto, S.; Urbani, S.; Servili, M. Fruit growth, yield and oil quality changes induced by deficit irrigation at different stages of olive fruit development. Agric. Water Manag. 2019, 212, 88–98. [Google Scholar] [CrossRef]
- Lavee, S.; Hanoch, E.; Wodner, M.; Abramowitch, H. The effect of predetermined deficit irrigation on the performance of cv Muhasan olives (Olea europaea L.) in the eastern coastal plain of Israel. Sci. Hortic. 2007, 112, 156–163. [Google Scholar] [CrossRef]
- Ahumada-Orellana, L.E.; Ortega-Farias, S.; Searles, P.S.; Retamanes, J.B. Yield and water productivity responses to irrigation cut-off strategies after fruit set using stem water potential thresholds in a super intensive olive orchard. Front. Plant Sci. 2017, 8, 1280. [Google Scholar] [CrossRef]
- Moriana, A.; Corell, M.; Girón, I.F.; Conejero, W.; Morales, D.; Torrecillas, A.; Moreno, F. Regulated deficit irrigation based on threshold values of trunk diameter fluctuation indicators in table olive trees. Sci. Hortic. 2013, 164, 102–111. [Google Scholar] [CrossRef]
- Girón, I.F.; Corell, M.; Martín-Palomo, M.J.; Galindo, A.; Torrecillas, A.; Moreno, F.; Moriana, A. Feasibility of trunk diameter fluctuations in the scheduling of regulated deficit irrigation for table olive trees without reference trees. Agric. Water Manag. 2015, 161, 114–126. [Google Scholar] [CrossRef]
- Corell, M.; Martín-Palomo, M.J.; Girón, I.; Andreu, L.; Galindo, A.; Centeno, A.; Pérez-López, D.; Moriana, A. Stem water potential-based regulated deficit irrigation scheduling for olive table trees. Agric. Water Manag. 2020, 242, 106418. [Google Scholar] [CrossRef]
- Corell, M.; Pérez-López, D.; Andreu, L.; Recena, R.; Centeno, A.; Galindo, A.; Moriana, A.; Martín-Palomo, M.J. Yield response of a mature hedgerow oil olive orchard to different levels of water stress during pit hardening. Agric. Water Manag. 2022, 261, 107374. [Google Scholar] [CrossRef]
- Hammani, S.B.M.; Costagli, G.; Rapoport, H.F. Cell and tissue dynamics of olive endocarp sclerification vary according to water availability. Physiol. Plant. 2013, 149, 571–582. [Google Scholar] [CrossRef] [PubMed]
- Hammami, S.B.M.; Manrique, T.; Rapoport, H.F. Cultivar based fruit size in olive depends on different tissue and cellular processes throughout growth. Sci. Hortic. 2011, 130, 445–451. [Google Scholar] [CrossRef]
- Rosati, A.; Caporali, S.; Hammani, S.B.M.; Moreno-Alías, I.; Rapoport, H. Fruit growth and sink strength in olive (Olea europea) are related to cell number, not to tissue size. Funct. Plant Biol. 2020, 47, 1098–1104. [Google Scholar] [CrossRef] [PubMed]
- Pérez-López, D.; Ribas, F.; Moriana, A.; Rapoport, H.; de Juan, A. Influence of temperature on the growth and development of olive (Olea europaea L) trees. J. Hort. Sci. Biotechnol. 2008, 83, 171–176. [Google Scholar] [CrossRef]
- Trentacoste, E.R.; Puertas, C.M.; Sadras, V.O. Modelling the intraspecific variation in the dinamics of fruit growth, oil and water concentration in olive (Olea europaea L.). Europ. J. Agron. 2012, 38, 83–93. [Google Scholar] [CrossRef]
- Martin-Palomo, M.J.; Corell, M.; Girón, I.; Andreu, L.; Galindo, A.; Centeno, A.; Pérez-López, D.; Moriana, A. Absence of yield reduction after controlled water stress during preharvest period in table olive trees. Agronomy 2020, 10, 258. [Google Scholar] [CrossRef]
- Rapoport, H.F.; Costagli, G.; Gucci, R. The effect of water deficit during early fruit development on olive fruit morphogenesis. J. Amer. Soc. Hort. Sci. 2004, 129, 121–127. [Google Scholar] [CrossRef]
- Rosati, A.; Zipancic, M.; Caporali, S.; Padula, G. Fruit weight is related to ovary weight in olive (Olea europaea L.). Sci. Hortic. 2009, 122, 399–403. [Google Scholar] [CrossRef]
- Benlloch-González, M.; Quintero, J.M.; Suárez, M.P.; Sánchez-Lucas, R.; Fernández-Escobar, R.; Benlloch, M. Effect of moderate high temperature on the vegetative growth and potassium allocation in olive plants. J. Plant Physiol. 2016, 207, 22–29. [Google Scholar] [CrossRef]
- Benlloch-González, M.; Sánchez-Lucas, R.; Bejaoui, M.A.; Benlloch, M.; Fernández-Escobar, R. Global warning effect on yield and fruit maturation of olive tres growing under field conditions. Sci. Hortic. 2019, 249, 162–167. [Google Scholar] [CrossRef]
- Garcia-Inza, G.P.; Castro, D.N.; Hall, A.J.; Rousseaux, M.C. Opposite oleic acid responses to temperature in oils from the seed and mesocarp of the olive fruit. Eur. J. Agron. 2016, 76, 138–147. [Google Scholar] [CrossRef]
- Garcia-Inza, G.P.; Castro, D.N.; Hall, A.J.; Rousseaux, M.C. Responses to temperature of fruit dry weight, oil concentration, and oil fatty acid composition in olive (Olea europaea L. var. ‘Arauco’). Eur. J. Agron. 2014, 54, 107–115. [Google Scholar] [CrossRef]
- Rallo, L.; Suarez, M.P. Seasonal distribution of dry matter within the olive fruit-bearing limb. Adv. Hort. Sci. 1989, 3, 55–59. [Google Scholar]
- Scorzal, R.; May, L.G.; Purnell, B.; Upchurch, B. Differences in number and area of mesocarp cells between small and large fruited peach cultivars. J. Am. Soc. Hortic. Sci. 1991, 116, 861–864. [Google Scholar] [CrossRef]
- McGarry, R.; Ozga, J.A.; Reinecke, D.M. Differences in fruit development among large and small fruited cultivars of Saskatoon (Amelanchier alnifolia Nutt). J. Am. Soc. Hortic. Sci. 2001, 126, 381–385. [Google Scholar] [CrossRef]
- Rosati, A.; Zipancic, M.; Caporali, S.; Paoletti, A. Fruit set is inversely related to flower and fruit weight in olive (Olea europaea L). Sci. Hortic. 2010, 126, 200–204. [Google Scholar] [CrossRef]
- Legave, J.M.; Blanke, M.; Christen, D.; Giovannini, D.; Mathieu, V.; Oger, R. A comprehensive overview of the spatial and temporal variability of apple bud dormancy release and blooming phenology in Western Europe. Int. J. Biometeorol. 2013, 57, 317–331. [Google Scholar] [CrossRef]
- Girón, I.F.; Corell, M.; Galindo, A.; Torrecillas, E.; Morales, D.; Dell’Amico, J.; Torrecillas, A.; Moreno, F.; Moriana, A. Changes in the physiological response between leaves and fruits during a moderate water stress in table olives. Agric. Water Manag. 2015, 148, 280–286. [Google Scholar] [CrossRef]
- Ben-Gal, A.; Ron, Y.; Yermiyahu, U.; Zipori, I.; Naoum, S.; Dag, A. Evaluation of regulated deficit irrigation strategies for oil olives: A case study for two modern Israeli cultivars. Agric. Water Manag. 2021, 245, 106577. [Google Scholar] [CrossRef]
- Gucci, R.; Lodolini, E.; Rapoport, H.F. Water déficit-induced changes in mesocarp cellular processes and the relationship between mesocarp and endocarp during olive fruit development. Tree Physiol. 2009, 29, 1575–1585. [Google Scholar] [CrossRef] [PubMed]
- Barranco, D. Variedades y Patrones. In El Cultivo del Olivo; Barranco, D., Fernández Escobar, R., Rallo, L., Eds.; Mundiprensa: Madrid, Spain, 1997; pp. 59–79. [Google Scholar]
- Pérez-López, D.; Ribas, F.; Moriana, A.; Olmedilla, N.; De Juan, A. The effect of irrigation schedules on the water relations and growth of a young olive (Olea europaea L.) orchard. Agric. Water Manag. 2007, 89, 297–304. [Google Scholar] [CrossRef]
- Sánchez-Piñero, M.; Martín-Palomo, M.J.; Andreu, L.; Moriana, A.; Corell, M. Evaluation of a simplified methodology to estimate the CWSI in olive orchards. Agric. Water Manag. 2022, 269, 107729. [Google Scholar] [CrossRef]
- Hsiao, T.C. Measurements of plant water status, Chapter 9. In Irrigation of Agricultural Crops; Steward, B.A., Nielsen, D.R., Eds.; Agronomy Monograph, 30; American Society of Agronomy: Madison, WI, USA, 1990; pp. 243–279. [Google Scholar]
- SIAR. Climatic Station Data in Spain. 2022. Available online: http://eportal.mapa.gob.es/websiar/SeleccionParametrosMap.aspx?dst=1 (accessed on 18 October 2022).
- Guo, L.; Dai, J.; Ranjitkar, S.; Yu, H.; Xu, J.; Luedeling, E. Chilling and heat requirements for flowering in temperate fruit trees. Int. J. Biometeorol. 2014, 58, 1195–1206. [Google Scholar] [CrossRef]
- Anderson, J.L.; Richardson, E.A.; Kesner, C.D. Validation of chill unit and flower bud phenology models for “Montmorency” sour cherry. Acta Hortic. 1986, 184, 71–78. [Google Scholar] [CrossRef]
- Bongi, G.; Palliotti, A. Olive, Chapter 6. In Temperate Crops; Schaffer, B., Andersen, P.C., Eds.; Handbook of environmental physiology of fruit crops; CRC Press: Boca Raton, FL, USA, 1994; Volume 1, pp. 165–187. [Google Scholar]





| Cultivar/Year | Location | a (MPa) | b (MPa Days−1) | c (days) | d (MPa) | a + d (MPa) | R2 |
|---|---|---|---|---|---|---|---|
| Cornicabra 2006 | Ciudad Real | 134 | 0.1477 | 61 | 2.95 | 137 | 0.99 |
| Cornicabra 2007 | Ciudad Real | 127 | 0.1626 | 64 | 4.53 | 131 | 0.99 |
| Cornicabra 2008 | Ciudad Real | 151 | 0.1097 | 65 | −4.90 | 146 | 0.94 |
| Cornicabra 2012 | Ciudad Real | 136 | 0.1472 | 64 | 1.89 | 138 | 0.73 |
| Cornicabra 2013 | Ciudad Real | 95 | 0.1192 | 64 | 1.19 | 96 | 0.55 |
| Arbequina 2008 | Ciudad Real | 109 | 0.1413 | 64 | 3.45 | 112 | 0.98 |
| Arbequina 2016 | Ciudad Real | 113 | 0.1500 | 58 | 2.09 | 115 | 0.56 |
| Arbequina 2017 | Ciudad Real | 85 | 0.1832 | 57 | 4.74 | 89 | 0.95 |
| Arbequina 2019 | Seville | 112 | 0.1434 | 66 | 2.56 | 114 | 0.88 |
| Manzanilla 2021 | Seville | 156 | 0.1266 | 75 | 10.56 | 166 | 0.91 |
| Manzanilla 2022 | Seville | 167 | 0.1102 | 68 | 1.49 | 168 | 0.95 |
| Cornicabra | 129 ab | 0.14 ± 0.02 | 64 ab | 1 ± 3.6 | 130 b | ||
| Arbequina | 105 b | 0.16 ± 0.02 | 61 b | 3 ± 1.2 | 108 b | ||
| Manzanilla | 162 a | 0.12 ± 0.02 | 71 a | 6 ± 7.5 | 167 a |
| Cultivar | Location | Full Bloom | Length | Lineal | Exponential | Cosine |
|---|---|---|---|---|---|---|
| LTT = 5 °C UPT = 40 °C | LTT = 5 °C UPT = 40 °C | LTT = 5 °C UPT = 40 °C OT = 25 °C | ||||
| Cornicabra | Ciudad Real | 25 May 2006 | 46 | 391 | 230 | 15,811 |
| Cornicabra | Ciudad Real | 7 June 2007 | 51 | 405 | 238 | 16,923 |
| Cornicabra | Ciudad Real | 7 June 2008 | 50 | 428 | 247 | 16,075 |
| Arbequina | Ciudad Real | 7 June 2008 | 47 | 400 | 231 | 15,044 |
| Cornicabra | Ciudad Real | 1 June 2012 | 51 | 470 | 267 | 16,604 |
| Cornicabra | Ciudad Real | 9 June 2013 | 47 | 441 | 251 | 14,581 |
| Arbequina | Ciudad Real | 8 June 2016 | 46 | 442 | 250 | 15,416 |
| Arbequina | Ciudad Real | 22 May 2017 | 46 | 427 | 247 | 15,746 |
| Arbequina | Seville | 25 April 2019 | 52 | 371 | 226 | 18,296 |
| Manzanilla | Seville | 17 April 2021 | 48 | 260 | 170 | 16,345 |
| Manzanilla | Seville | 27 April 2022 | 53 | 420 | 247 | 17,856 |
| Cornicabra | Ciudad Real | 4 June | 49 | 427 | 246 | 15,999 |
| Arbequina | Ciudad Real | 2 June | 46 | 423 | 243 | 15,402 |
| Arbequina | Seville | 25 April | 52 | 371 | 226 | 18,296 |
| Manzanilla | Seville | 23 April | 51 | 340 | 208 | 17,100 |
| Average | 48.8 ± 2.6 | 405 ± 55 | 237 ± 25 | 16,245 ± 1130 | ||
| CV | 5.4 | 13.7 | 10.6 | 7,0 |
| Correlation Coefficient (r) | R2 | Mean Square Error | Number of Data | |
|---|---|---|---|---|
| R Weight vs. Lineal Thermal time | −0.47 | 0.26 | 0.028 | 9 |
| R Weight vs. Exp Thermal time | −0.53 | 0.36 | 0.025 | 9 |
| R Weight vs. Cos Thermal time | −0.21 | 0.11 | 0.034 | 9 |
| R Volume vs. Lineal Thermal time | −0.45 | 0.21 | 0.022 | 8 |
| R Volume vs. Exp Thermal time | −0.49 | 0.24 | 0.021 | 8 |
| R Volume vs. Cos Thermal time | −0.19 | 0.04 | 0.027 | 8 |
| R Weight vs. R Volume | 0.71 | 0.50 | 0.017 | 8 |
| Cultivar | Locations | Length | Lineal | Exponential | Cosine |
|---|---|---|---|---|---|
| Season | LTT = 5 °C UPT = 40 °C | LTT = 5 °C UPT = 40 °C | LTT = 5 °C UPT = 40 °C OT = 25 °C | ||
| Cornicabra | Ciudad Real 2006 | 35 | 419 | 229 | 10,575 |
| Cornicabra | Ciudad Real 2007 | 31 | 307 | 177 | 10,456 |
| Cornicabra | Ciudad Real 2008 | 42 | 383 | 218 | 13,786 |
| Arbequina | Ciudad Real 2008 | 38 | 368 | 206 | 12,098 |
| Cornicabra | Ciudad Real 2012 | 33 | 359 | 201 | 10,006 |
| Cornicabra | Ciudad Real 2013 | 41 | 385 | 223 | 13,340 |
| Arbequina | Ciudad Real 2016 | 31 | 352 | 195 | 10,445 |
| Arbequina | Ciudad Real 2017 | 26 | 293 | 164 | 8220 |
| Arbequina | Seville 2019 | 33 | 327 | 186 | 12,143 |
| Manzanilla | Seville 2021 | 50 | 469 | 270 | 17,806 |
| Manzanilla | Seville 2022 | 45 | 342 | 204 | 15,387 |
| Cornicabra | Ciudad Real | 37 | 371 | 210 | 11,633 |
| Arbequina | Ciudad Real | 32 | 338 | 188 | 10,254 |
| Arbequina | Seville | 33 | 327 | 186 | 12,143 |
| Manzanilla | Seville | 47 | 405 | 237 | 16,597 |
| Average | 36.9 ± 7.0 | 364 ± 50 | 207 ± 29 | 12,206 ± 2736 | |
| CV | 19.0 | 13.7 | 13.9 | 22.4 |
| Best Fit | R2 | Error | N | MSE |
|---|---|---|---|---|
| WH = 0.129 + 2.799 × W1 | 0.78 *** | 0.164 | 81 | 0.027 |
| VH = 2.482 × V1 | 0.87 *** | 0.262 | 71 | 0.069 |
| BEST Fit | R2 | Error | N | MSE |
|---|---|---|---|---|
| VH = 3.781 × V1 | 0.71 *** | 0.408 | 32 | 0.167 |
| VH = 1.169 + 2.916 × V1 − 0.189 × FL | 0.73 *** | 0.391 | 32 | 0.153 |
| FS = 475.6 − 215.6 × V1 | 0.65 *** | 28.3 | 32 | 799.2 |
| FS = 351.2 − 127.2 × V1 + 23.7 × FL | 0.80 *** | 21.0 | 32 | 440.4 |
| SEVILLE | CIUDAD REAL | |||||
|---|---|---|---|---|---|---|
| T Max | T Min | Rain | T Max | T Min | Rain | |
| January | 19.88 | −0.73 | 52 | 16.70 | −6.12 | 37 |
| February | 22.49 | 0.44 | 52 | 19.27 | −5.28 | 39 |
| March | 27.81 | 1.44 | 58 | 23.68 | −3.51 | 46 |
| April | 30.37 | 5.95 | 62 | 26.31 | −0.26 | 63 |
| May | 34.71 | 8.27 | 32 | 32.32 | 1.66 | 31 |
| June | 38.91 | 11.31 | 3 | 38.00 | 6.53 | 15 |
| July | 40.23 | 14.08 | 0 | 39.49 | 10.81 | 3 |
| August | 41.69 | 13.84 | 5 | 39.70 | 10.02 | 6 |
| September | 38.02 | 11.30 | 29 | 35.05 | 6.39 | 33 |
| October | 32.50 | 7.64 | 63 | 28.95 | 0.94 | 51 |
| November | 26.13 | 2.50 | 74 | 21.77 | −3.62 | 52 |
| December | 20.77 | 0.11 | 67 | 16.70 | −5.86 | 45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Piñero, M.; Martín-Palomo, M.J.; Moriana, A.; Corell, M.; Pérez-López, D. Endocarp Development Study in Full Irrigated Olive Orchards and Impact on Fruit Features at Harvest. Plants 2022, 11, 3541. https://doi.org/10.3390/plants11243541
Sánchez-Piñero M, Martín-Palomo MJ, Moriana A, Corell M, Pérez-López D. Endocarp Development Study in Full Irrigated Olive Orchards and Impact on Fruit Features at Harvest. Plants. 2022; 11(24):3541. https://doi.org/10.3390/plants11243541
Chicago/Turabian StyleSánchez-Piñero, Marta, María José Martín-Palomo, Alfonso Moriana, Mireia Corell, and David Pérez-López. 2022. "Endocarp Development Study in Full Irrigated Olive Orchards and Impact on Fruit Features at Harvest" Plants 11, no. 24: 3541. https://doi.org/10.3390/plants11243541
APA StyleSánchez-Piñero, M., Martín-Palomo, M. J., Moriana, A., Corell, M., & Pérez-López, D. (2022). Endocarp Development Study in Full Irrigated Olive Orchards and Impact on Fruit Features at Harvest. Plants, 11(24), 3541. https://doi.org/10.3390/plants11243541








