A Fractional-Order Archimedean Spiral Moth–Flame Optimization Strategy to Solve Optimal Power Flows
Abstract
1. Introduction
- Utilizing the strengths of FO-AMFO, a novel application of the fractional evolutionary approach for ORPD is proposed.
- The design scheme is successfully applied to ORPD problems in order to minimize power losses while meeting load demand and operational constraints.
- The algorithm’s performance is determined by statistical findings in the form of probability plots, learning curves, and histogram analysis, which demonstrate the algorithm’s stability, resilience, and consistency as a precise and efficient optimization mechanism.
2. Problem Formulation
2.1. System Constraints
2.2. Tap Limits
2.3. Voltage Generation Limits
2.4. Reactors Limits
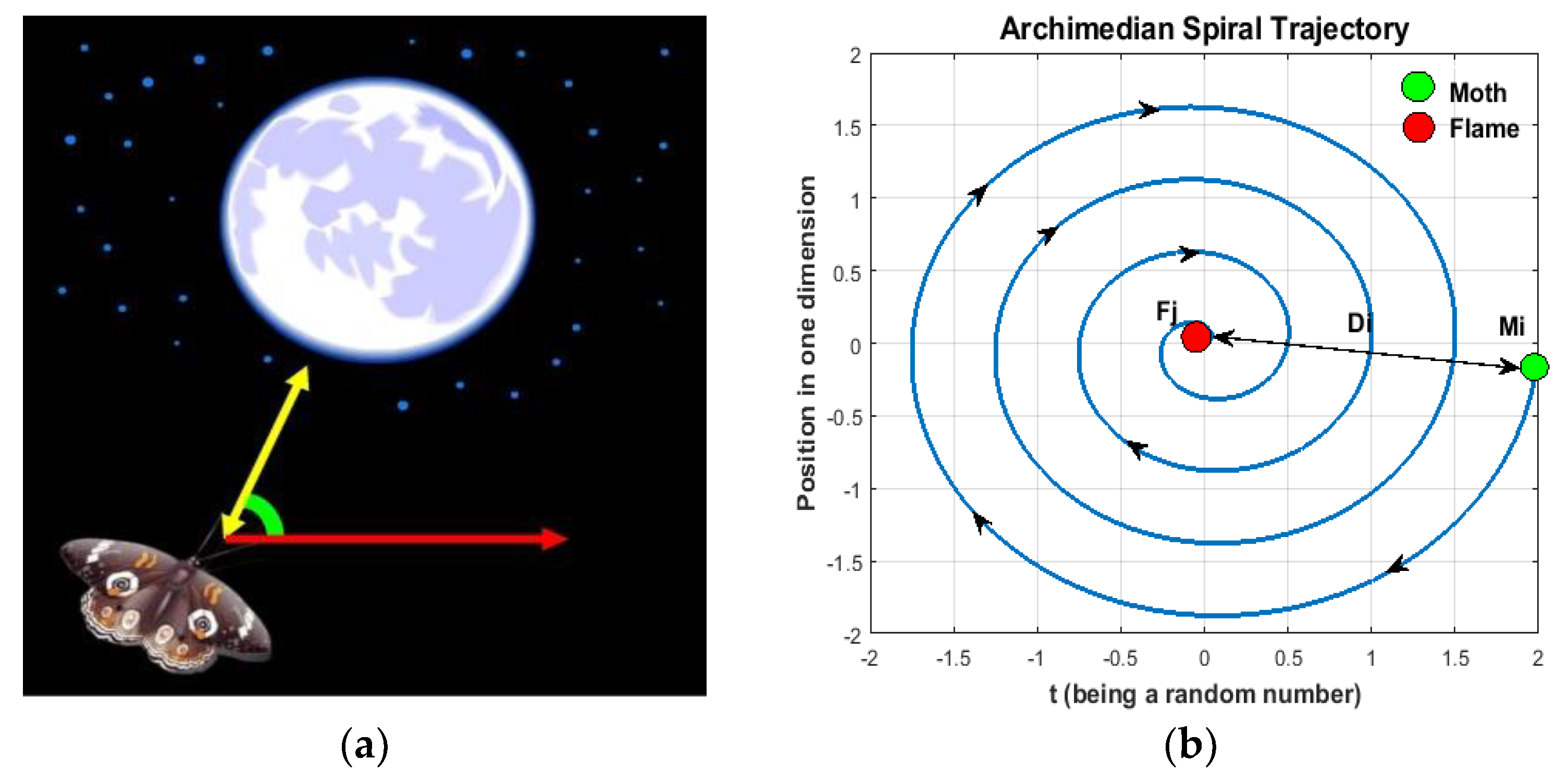
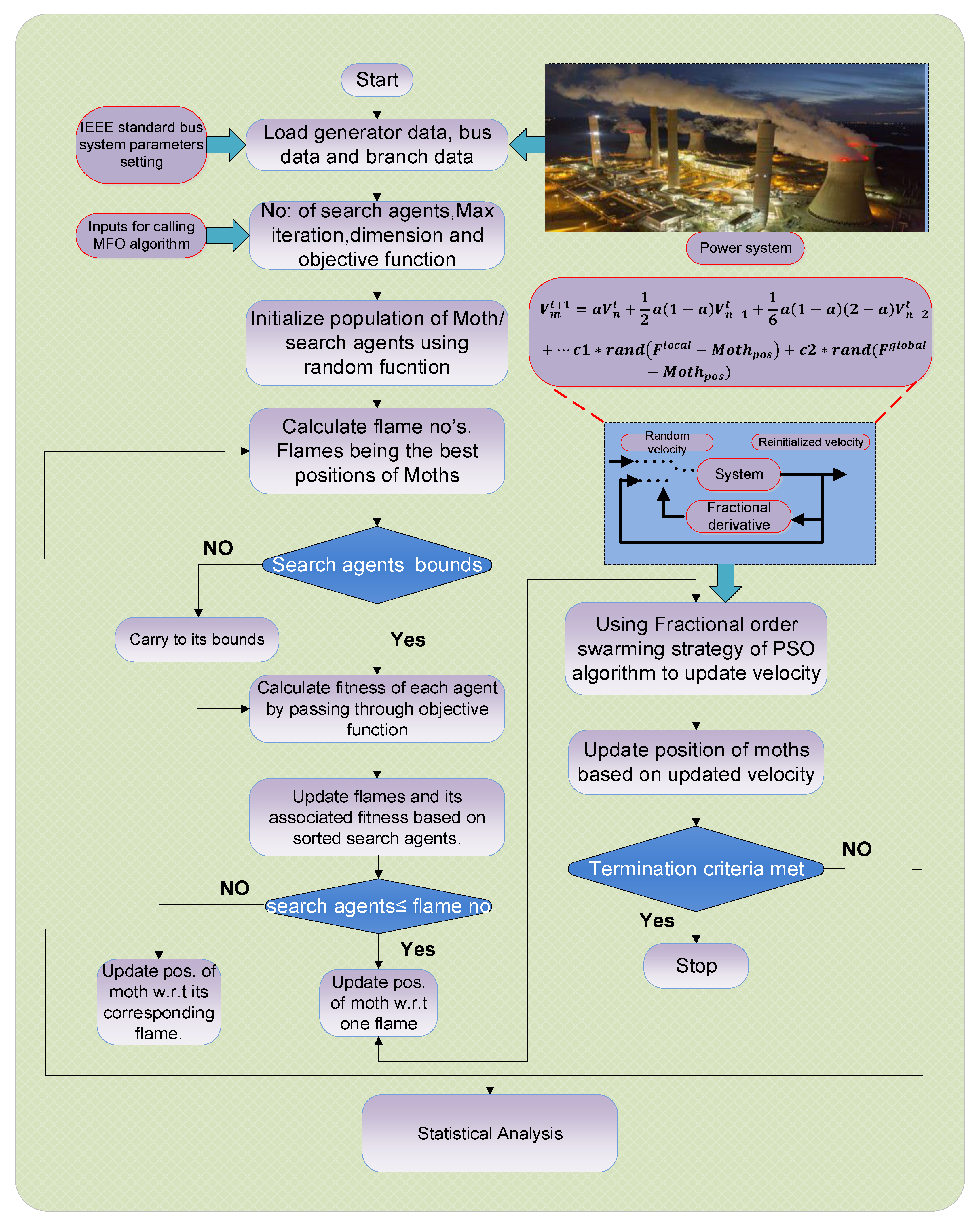
3. Methodology
4. Results and Discussion
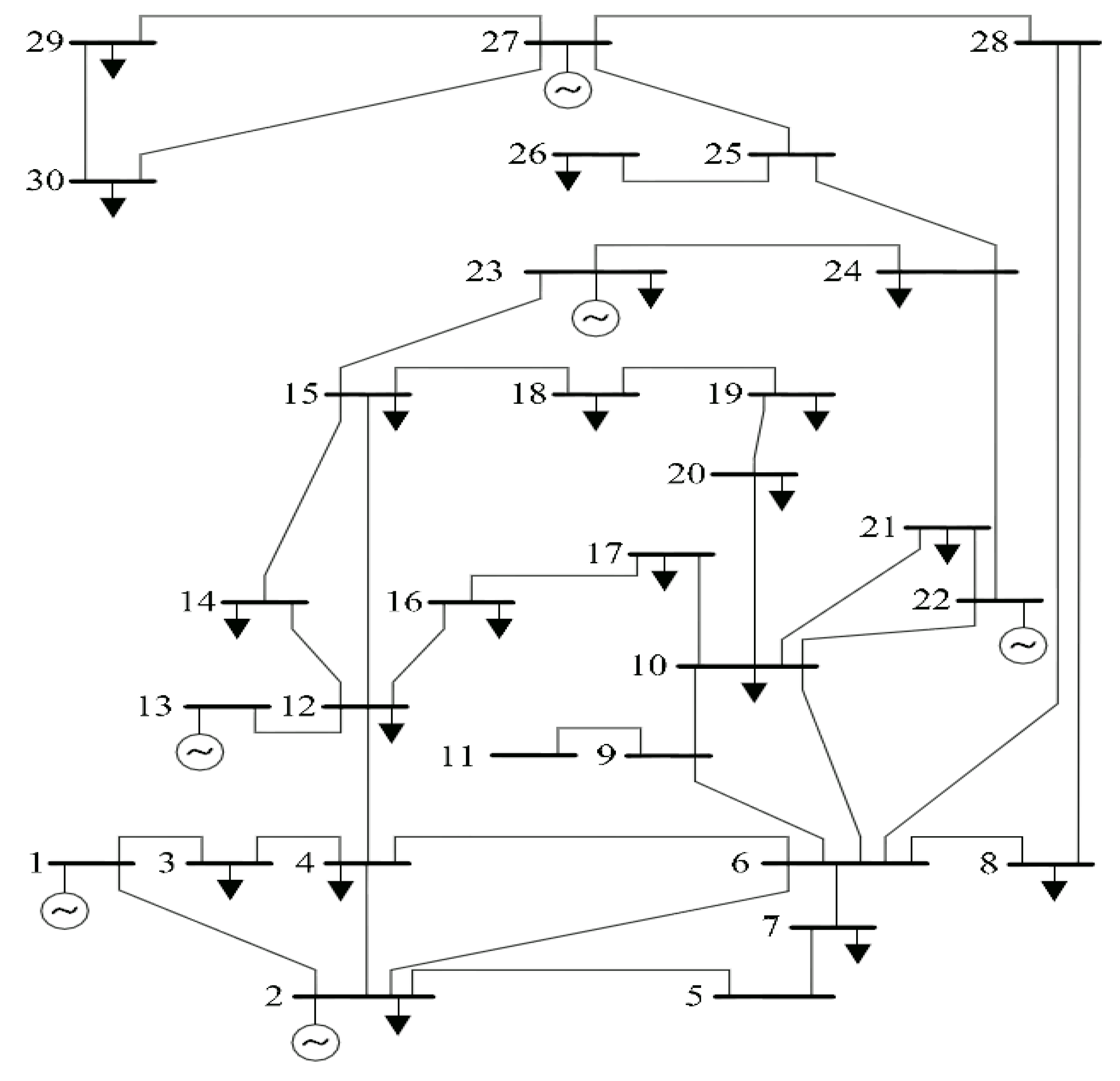
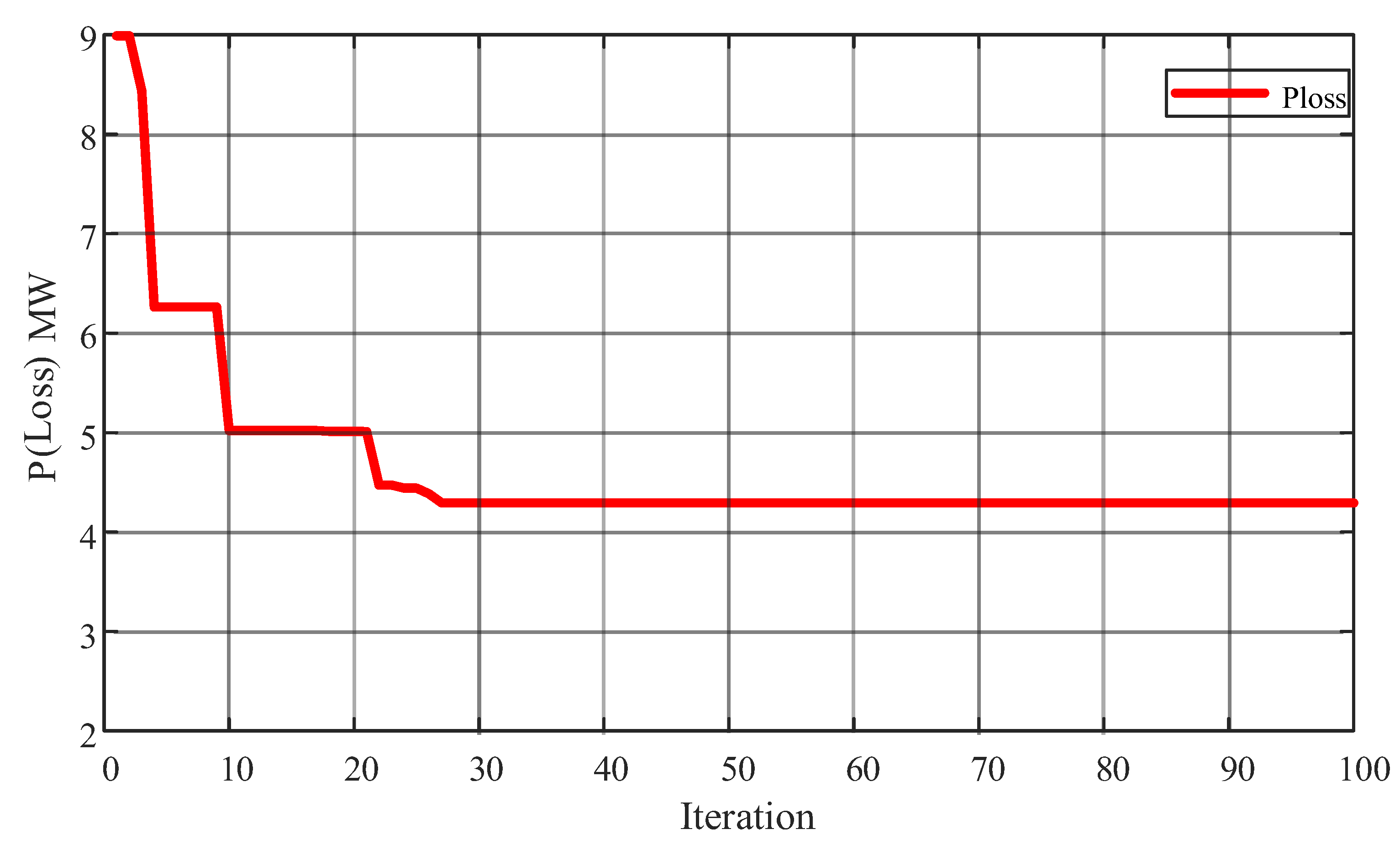
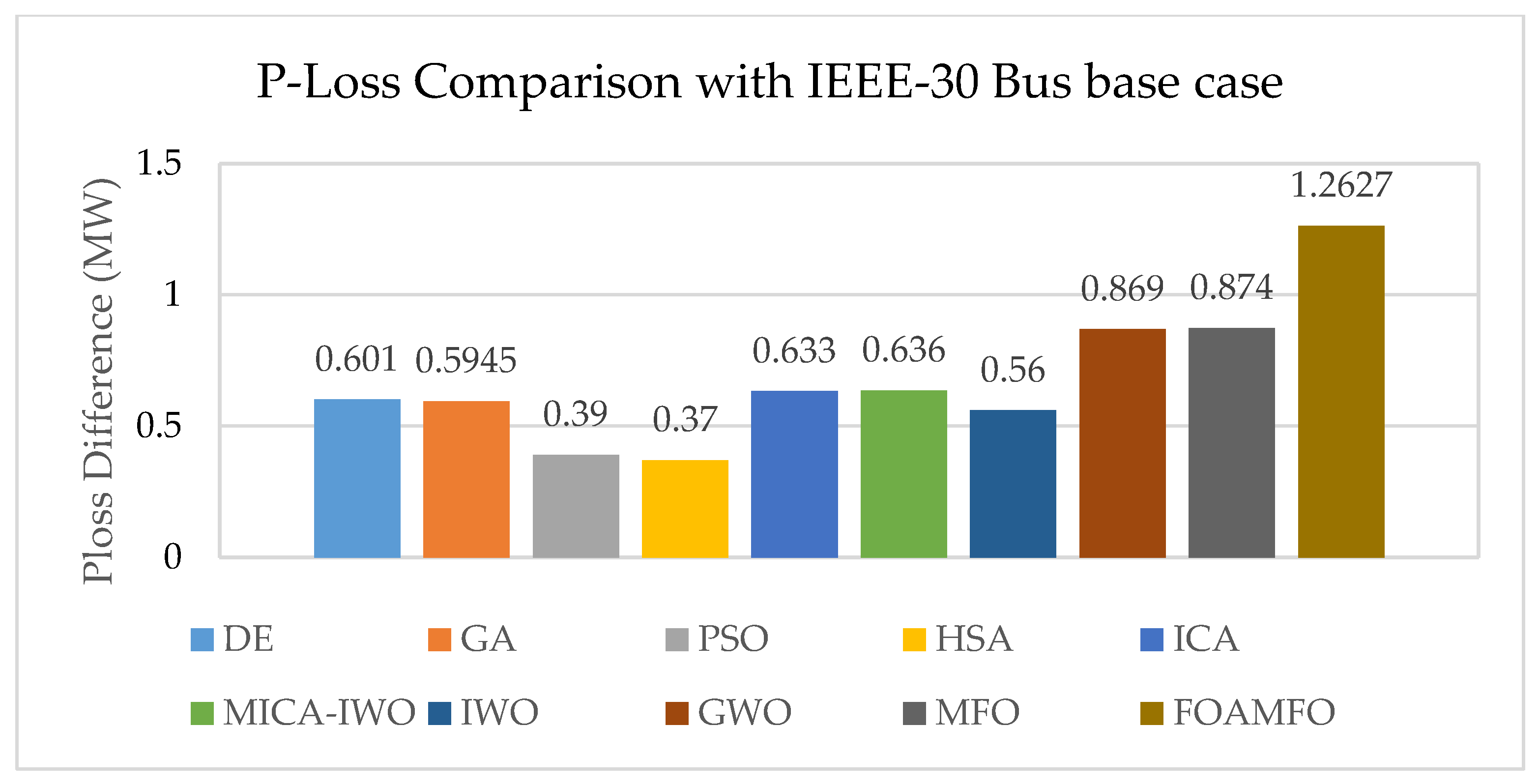
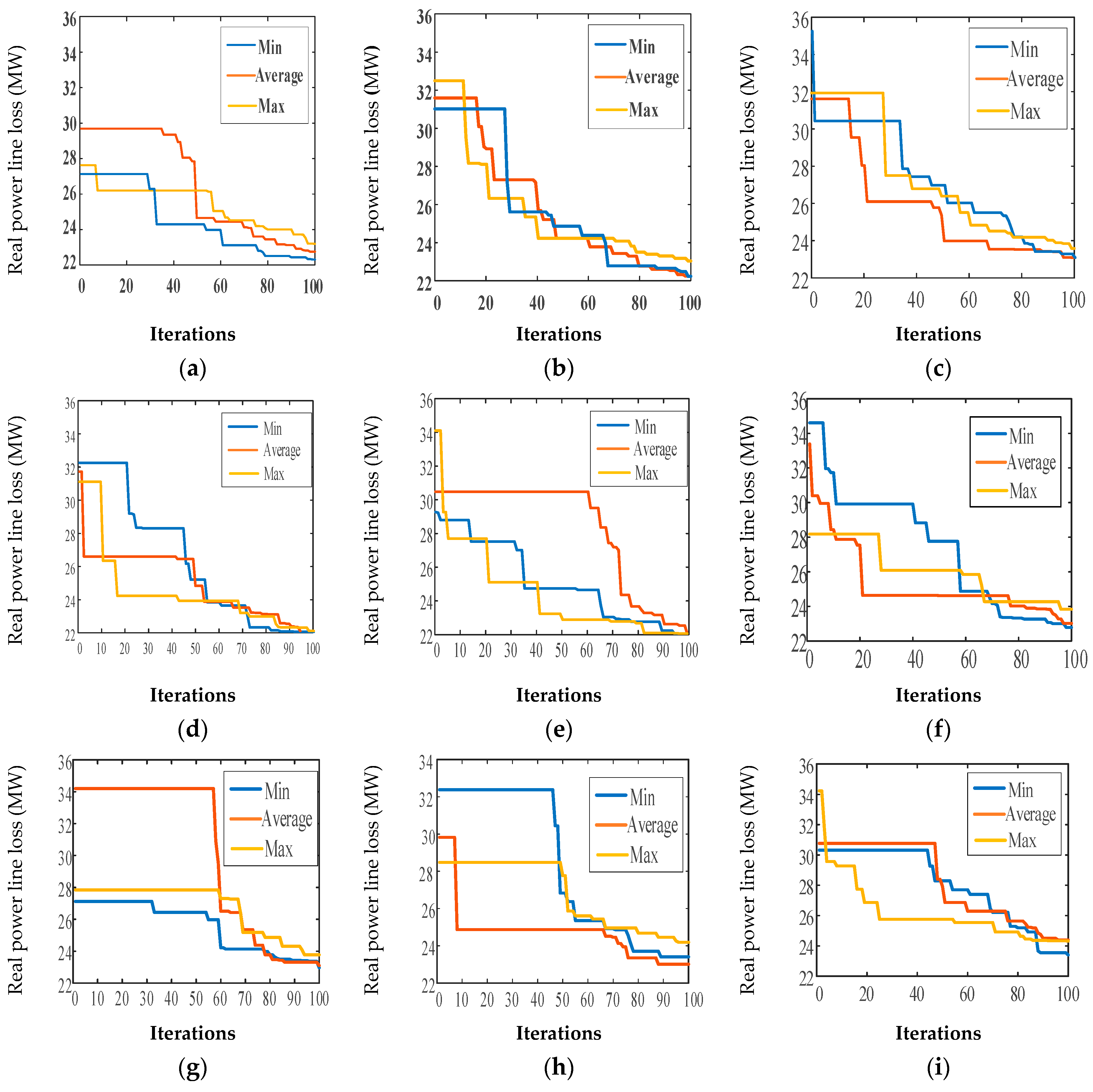
4.1. Case 1: ORPD 13 Variables for a 30-Bus IEEE System
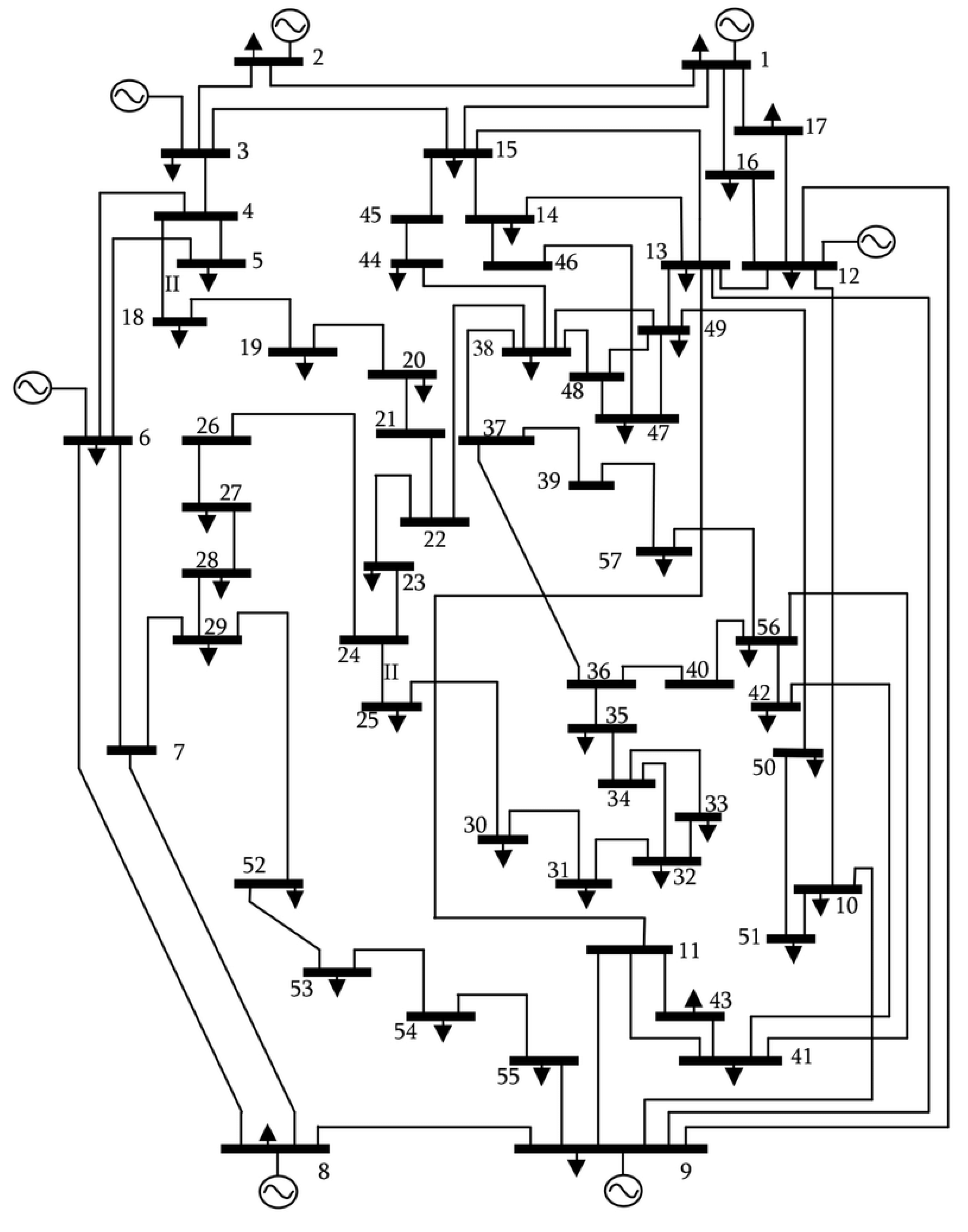
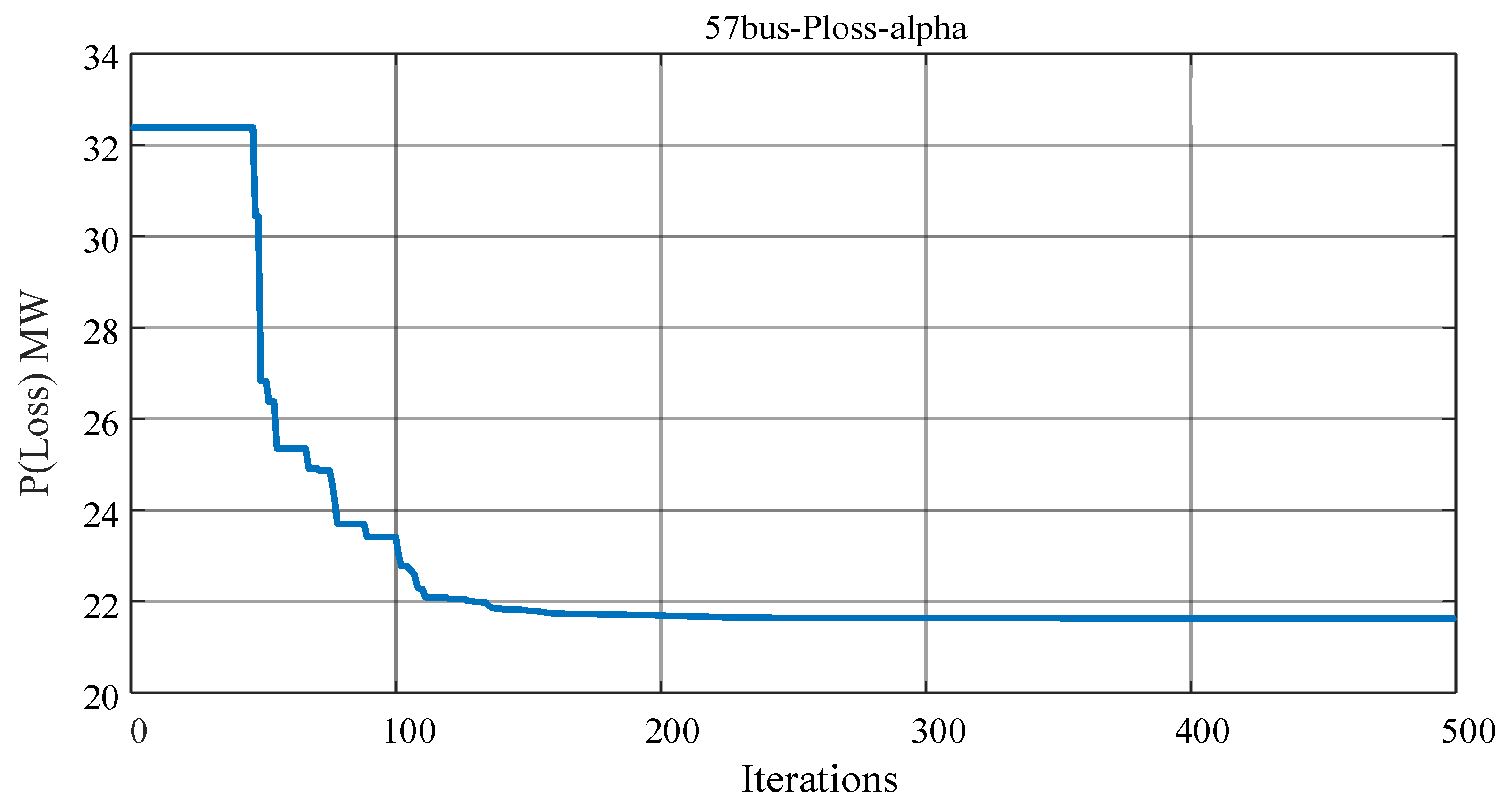
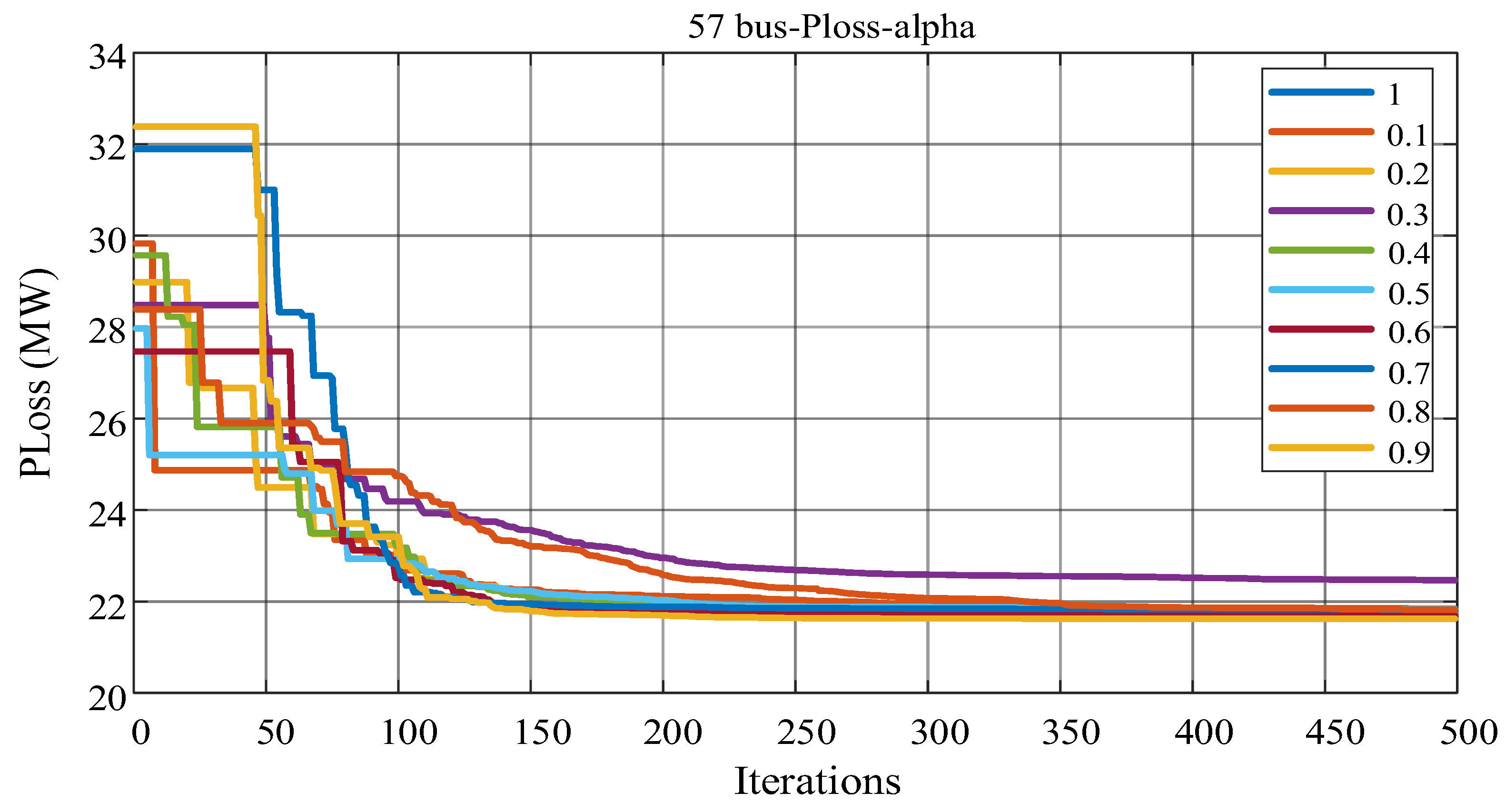
4.2. Case 2: ORPD for the IEEE 57-Bus System with 25 Control Variables
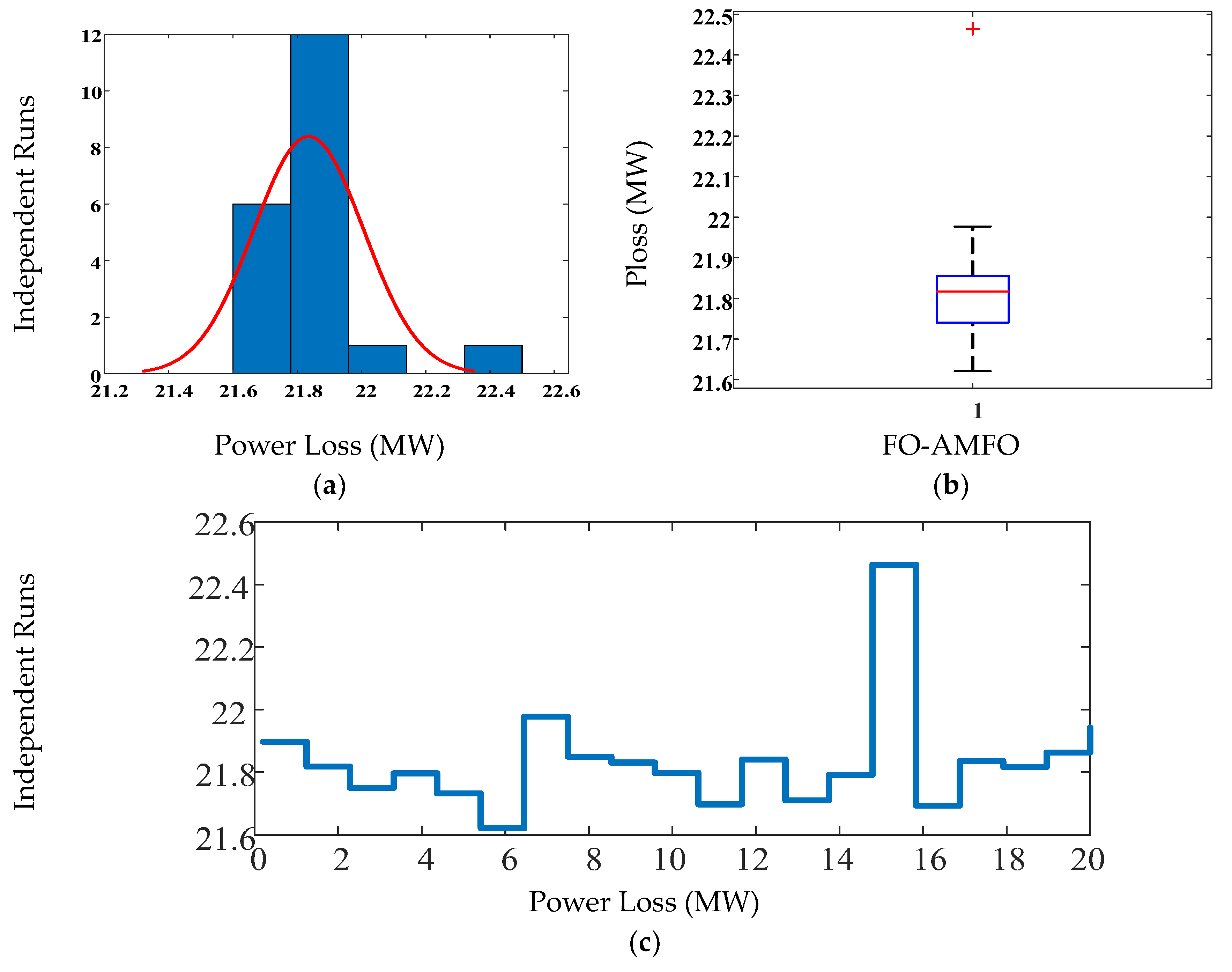
4.3. Comparative Analysis through Statistics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, X.; Yu, X.; Lu, Y.; Sheng, J. Economic and emission dispatch using ensemble multi-objective differential evolution algorithm. Sustainability 2018, 10, 418. [Google Scholar] [CrossRef]
- Jiang, S.; Ji, Z.; Wang, Y. A novel gravitational acceleration enhanced particle swarm optimization algorithm for wind–thermal economic emission dispatch problem considering wind power availability. Int. J. Electr. Power Energy Syst. 2015, 73, 1035–1050. [Google Scholar] [CrossRef]
- Jadoun, V.K.; Pandey, V.C.; Gupta, N.; Niazi, K.R.; Swarnkar, A. Integration of renewable energy sources in dynamic economic load dispatch problem using an improved fireworks algorithm. IET Renew. Power Gener. 2018, 12, 1004–1011. [Google Scholar] [CrossRef]
- Santra, D.; Sarker, K.; Mukherjee, A.; Mondal, S. Combined economic emission and load dispatch using hybrid metaheuristics. Int. J. Hybrid Intell. 2019, 1, 211–238. [Google Scholar] [CrossRef]
- Sinha, N.; Chakrabarti, R.; Chattopadhyay, P. Evolutionary programming techniques for economic load dispatch. IEEE Trans. Evol. Comput. 2003, 7, 83–94. [Google Scholar] [CrossRef]
- Gopalakrishnan, R.; Krishnan, A. An efficient technique to solve combined economic and emission dispatch problem using modified Ant colony optimization. Sadhana 2013, 38, 545–556. [Google Scholar] [CrossRef]
- Faris, H.; Aljarah, I.; Al-Betar, M.A.; Mirjalili, S. Grey wolf optimizer: A review of recent variants and applications. Neural Comput. Appl. 2017, 30, 413–435. [Google Scholar] [CrossRef]
- Manton, J. Optimization algorithms exploiting unitary constraints. IEEE Trans. Signal Process. 2002, 50, 635–650. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, K.; Zhang, X.; Su, L.; Ngai, E.; Liu, M. Application of evolutionary computation for rule discovery in stock algorithmic trading: A literature review. Appl. Soft Comput. 2015, 36, 534–551. [Google Scholar] [CrossRef]
- Askarzadeh, A. Solving electrical power system problems by harmony search: A review. Artif. Intell. Rev. 2016, 47, 217–251. [Google Scholar] [CrossRef]
- Binitha, S.; Sathya, S.S. A survey of bio inspired optimization algorithms. Int. J. Soft Comput. Eng. 2012, 2, 137–151. [Google Scholar]
- Zhang, J.; Wu, Y.; Guo, Y.; Wang, B.; Wang, H.; Liu, H. A hybrid harmony search algorithm with differential evolution for day-ahead scheduling problem of a microgrid with consideration of power flow constraints. Appl. Energy 2016, 183, 791–804. [Google Scholar] [CrossRef]
- Naderi, E.; Azizivahed, A.; Narimani, H.; Fathi, M.; Narimani, M.R. A comprehensive study of practical economic dispatch problems by a new hybrid evolutionary algorithm. Appl. Soft Comput. 2017, 61, 1186–1206. [Google Scholar] [CrossRef]
- Neto, J.X.V.; Reynoso-Meza, G.; Ruppel, T.H.; Mariani, V.C.; dos Santos Coelho, L. Solving non-smooth economic dispatch by a new combination of continuous GRASP algorithm and differential evolution. Int. J. Electr. Power Energy Syst. 2017, 84, 13–24. [Google Scholar] [CrossRef]
- Khan, B.S.; Raja, M.A.Z.; Qamar, A.; Chaudhary, N.I. Design of moth flame optimization heuristics for integrated power plant system containing stochastic wind. Appl. Soft Comput. 2021, 104, 107193. [Google Scholar] [CrossRef]
- Muhammad, Y.; Khan, R.; Ullah, F.; Rehman, A.U.; Aslam, M.S.; Raja, M.A.Z. Design of fractional swarming strategy for solution of optimal reactive power dispatch. Neural Comput. Appl. 2019, 32, 10501–10518. [Google Scholar] [CrossRef]
- El Ela, A.A.; Abido, M.A.; Spea, S.R. Differential evolution algorithm for optimal reactive power dispatch. Electr. Power Syst. Res. 2011, 81, 458–464. [Google Scholar] [CrossRef]
- Mahadevan, K.; Kannan, P. Comprehensive learning particle swarm optimization for reactive power dispatch. Appl. Soft Comput. 2010, 10, 641–652. [Google Scholar] [CrossRef]
- Khazali, A.; Kalantar, M. Optimal reactive power dispatch based on harmony search algorithm. Int. J. Electr. Power Energy Syst. 2011, 33, 684–692. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghavidel, S.; Ghanbarian, M.M.; Habibi, A. A new hybrid algorithm for optimal reactive power dispatch problem with discrete and continuous control variables. Appl. Soft Comput. 2014, 22, 126–140. [Google Scholar] [CrossRef]
- Mandal, B.; Roy, P.K. Optimal reactive power dispatch using quasi-oppositional teaching learning based optimization. Int. J. Electr. Power Energy Syst. 2013, 53, 123–134. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z.; Mohamed, M.R.; Aliman, O. Using the gray wolf optimizer for solving optimal reactive power dispatch problem. Appl. Soft Comput. 2015, 32, 286–292. [Google Scholar] [CrossRef]
- Mei, R.N.S.; Sulaiman, M.H.; Mustaffa, Z.; Daniyal, H. Optimal reactive power dispatch solution by loss minimization using moth-flame optimization technique. Appl. Soft Comput. 2017, 59, 210–222. [Google Scholar] [CrossRef]
- Ghamisi, P.; Couceiro, M.S.; Benediktsson, J.A. A Novel Feature Selection Approach Based on FODPSO and SVM. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2935–2947. [Google Scholar] [CrossRef]
- Ates, A.; Alagoz, B.B.; Kavuran, G.; Yeroglu, C. Implementation of fractional order filters discretized by modified Fractional Order Darwinian Particle Swarm Optimization. Measurement 2017, 107, 153–164. [Google Scholar] [CrossRef]
- Couceiro, M.S.; Rocha, R.P.; Ferreira, N.M.F.; Machado, J.A.T. Introducing the fractional-order Darwinian PSO. Signal Image Video Process. 2012, 6, 343–350. [Google Scholar] [CrossRef]
- Shahri, E.S.A.; Alfi, A.; Machado, J.T. Fractional fixed-structure H∞ controller design using augmented Lagrangian particle swarm optimization with fractional order velocity. Appl. Soft Comput. 2019, 77, 688–695. [Google Scholar] [CrossRef]
- Machado, J.T.; Kiryakova, V. The chronicles of fractional calculus. Fract. Calc. Appl. Anal. 2017, 20, 307–336. [Google Scholar] [CrossRef]
- Ghamisi, P.; Couceiro, M.S.; Martins, F.M.L.; Benediktsson, J.A. Multilevel Image Segmentation Based on Fractional-Order Darwinian Particle Swarm Optimization. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2382–2394. [Google Scholar] [CrossRef]
- Zhu, Q.; Yuan, M.; Chen, Y.; Liu, Y.-L.; Chen, W.-D.; Wang, H.-R. Research and application on fractional-order Darwinian PSO based adaptive extended kalman filtering algorithm. IAES Int. J. Robot. Autom. 2014, 3, 245–251. [Google Scholar] [CrossRef]
- Yokoya, N.; Ghamisi, P. Land-cover monitoring using time-series hyperspectral data via fractional-order darwinian particle swarm optimization segmentation. In Proceedings of the 2016 8th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Los Angeles, CA, USA, 21–24 August 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar]
- Wang, Y.-Y.; Zhang, H.; Qiu, C.-H.; Xia, S.-R. A Novel Feature Selection Method Based on Extreme Learning Machine and Fractional-Order Darwinian PSO. Comput. Intell. Neurosci. 2018, 2018, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Paliwal, K.; Singh, S.; Gaba, P. Feature selection approach of hyperspectral image using GSA-FODPSO-SVM. In Proceedings of the 2017 International Conference on Computing, Communication and Automation (ICCCA), Greater Noida, India, 5–6 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1070–1075. [Google Scholar]
- Łegowski, A.; Niezabitowski, M. Robot path control based on PSO with fractional-order velocity. In Proceedings of the 2016 International Conference on Robotics and Automation Engineering (ICRAE), Jeju, Korea, 27–29 August 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 21–25. [Google Scholar]
- Kuttomparambil Abdulkhader, H.; Jacob, J.; Mathew, A.T. Fractional-order lead-lag compensator-based multi-band power system stabiliser design using a hybrid dynamic GA-PSO algorithm. IET Gener. Transm. Distrib. 2018, 12, 3248–3260. [Google Scholar] [CrossRef]
- Kosari, M.; Teshnehlab, M. Non-linear fractional-order chaotic systems identification with approximated fraction-al-order derivative based on a hybrid particle swarm optimization-genetic algorithm method. J. AI Data Min. 2018, 6, 365–373. [Google Scholar]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Brzeziński, D.W.; Ostalczyk, P. About accuracy increase of fractional order derivative and integral computations by applying the Grünwald–Letnikov formula. Commun. Nonlinear Sci. Numer. Simul. 2016, 40, 151–162. [Google Scholar] [CrossRef]
- Dai, C.; Chen, W.; Zhu, Y.; Zhang, X. Seeker Optimization Algorithm for Optimal Reactive Power Dispatch. IEEE Trans. Power Syst. 2009, 24, 1218–1231. [Google Scholar] [CrossRef]
- Villa-Acevedo, W.M.; López-Lezama, J.M.; Valencia-Velásquez, J.A. A Novel Constraint Handling Approach for the Optimal Reactive Power Dispatch Problem. Energies 2018, 11, 2352. [Google Scholar] [CrossRef]
- Babu, R.; Raj, S.; Dey, B.; Bhattacharyya, B. Optimal reactive power planning using oppositional grey wolf optimization by considering bus vulnerability analysis. Energy Convers. Econ. 2021, 3, 38–49. [Google Scholar] [CrossRef]
- Khan, N.H.; Wang, Y.; Tian, D.; Raja, M.A.Z.; Jamal, R.; Muhammad, Y. Design of Fractional Particle Swarm Optimization Gravitational Search Algorithm for Optimal Reactive Power Dispatch Problems. IEEE Access 2020, 8, 146785–146806. [Google Scholar] [CrossRef]


| Functions | GSA [37] | PSO [37] | MFO [37] | FO-AMFO |
|---|---|---|---|---|
| 608.2432 | 1.321140 | 0.0001170 | 0.0099567 | |
| 22.7534 | 7.715640 | 0.0006390 | 0.0000077 | |
| 135760.7 | 736.3190 | 696.73090 | 3.761800 | |
| 78.7854 | 12.97654 | 70.686460 | 24.662000 | |
| 741.005 | 77360.83 | 139.14870 | 97.876000 | |
| 3080.67 | 286.6585 | 0.0001130 | 0.00000408 | |
| 0.11256 | 1.037426 | 0.0911550 | 0.0279000 | |
| −2352.36 | −3572.000 | −8496.780 | −3065.6000 | |
| 31.00015 | 124.1962 | 84.600090 | 19.996000 | |
| 0.048679 | 0.021654 | 0.0190800 | 0.296200 |
| Characteristics | IEEE 30 Bus 13 Variables |
|---|---|
| Total Buses | 30 |
| Load Buses | 24 |
| Total Generators | 6 |
| Total Transformers | 4 |
| Total Capacitors | 9 |
| Total Reactors | 0 |
| Total Branches | 41 |
| Control Variables | Reported Results Proposed | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| D-E [17] | G-A [18] | (PSO) [19] | HS-A [19] | MICA-(IWO) [20] | IC-A [20] | I-WO [21] | G-WO [22] | (MFO) [23] | FO- (AMFO) | |
| Vg-1 | 1.095 | 1.072 | 1.031 | 1.072 | 1.079 | 1.078 | 1.069 | 1.100 | 1.100 | 1.028 |
| Vg-2 | 1.085 | 1.063 | 1.011 | 1.062 | 1.070 | 1.069 | 1.060 | 1.096 | 1.094 | 1.021 |
| Vg-5 | 1.062 | 1.037 | 1.022 | 1.039 | 1.048 | 1.069 | 1.036 | 1.080 | 1.075 | 0.985 |
| Vg-8 | 1.065 | 1.044 | 1.003 | 1.042 | 1.048 | 1.047 | 1.038 | 1.080 | 1.771 | 0.990 |
| Vg-11 | 1.026 | 1.013 | 0.974 | 1.031 | 1.075 | 1.034 | 1.029 | 1.093 | 1.086 | 1.002 |
| Vg-13 | 1.014 | 1.089 | 0.998 | 1.068 | 1.070 | 1.071 | 1.055 | 1.100 | 1.100 | 1.028 |
| Th6-9 | 1.017 | 1.022 | 0.970 | 1.010 | 1.030 | 1.080 | 1.050 | 1.040 | 1.041 | 1.054 |
| Th6-10 | 0.979 | 0.991 | 1.020 | 1 | 0.990 | 0.950 | 0.960 | 0.950 | 0.950 | 1.045 |
| Th4-12 | 0.977 | 0.996 | 1.010 | 0.990 | 1 | 1 | 0.970 | 0.950 | 0.955 | 0.922 |
| Th27-28 | 1.008 | 0.97 | 0.990 | 0.970 | 0.980 | 0.970 | 0.970 | 0.950 | 0.957 | 0.938 |
| Q-c3 | 20.223 | 5.350 | 17 | 34 | −7 | −6 | 8 | 12 | 7.103 | 30 |
| Q-c10 | 9.584 | 36 | 13 | 12 | 23 | 36 | 35 | 30 | 30.796 | 29.870 |
| Q-c24 | 13.029 | 12.417 | 23 | 10 | 12 | 11 | 11 | 8 | 9.898 | 30 |
| PL | 4.88 | 4.87 | 5.88 | 5.10 | 4.84 | 4.84 | 4.92 | 4.61 | 4.60 | 4.219 |
| Characteristics | IEEE 57-Bus 25 Variables |
|---|---|
| Total Buses | 57 |
| Load Buses | 45 |
| Total Generators | 7 |
| Total Transformers | 17 |
| Total Capacitors | 3 |
| Total Reactors | 15 |
| Total Branches | 80 |
| Control Variables | Base Case [16] | FO- DPSO [16] | SOA [39] | MFO [15] | IWO [20] | CLPS [40] | GWO [41] | FPSO-GSA [42] | FO-AMFO |
|---|---|---|---|---|---|---|---|---|---|
| V-G (1) | 1.040 | 1.04 | 1.060 | 1.060 | 1.06 | 1.054 | 1.060 | 1.100 | 1.100 |
| V-G (2) | 1.011 | 1.029 | 1.058 | 1.058 | 1.059 | 1.052 | 1.056 | 1.098 | 1.0991 |
| V-G (3) | 0.985 | 1.009 | 1.043 | 1.046 | 1.047 | 1.033 | 1.037 | 1.087 | 1.0889 |
| V-G (6) | 0.980 | 0.977 | 1.035 | 1.042 | 1.038 | 1.031 | 1.020 | 1.080 | 1.0832 |
| V-G (8) | 1.050 | 0.985 | 1.054 | 1.060 | 1.059 | 1.049 | 1.044 | 1.100 | 1.1000 |
| V-G (9) | 0.980 | 0.967 | 1.036 | 1.042 | 1.027 | 1.030 | 1.029 | 1.084 | 1.0848 |
| V-G (12) | 1.015 | 0.908 | 1.033 | 1.037 | 1.037 | 1.034 | 1.031 | 0.960 | 1.0808 |
| T-TS (4-18) | 0.970 | 0.9 | 1 | 0.950 | 1.05 | 0.990 | 0.984 | 1.007 | 0.900 |
| T-TS (4-18) | 0.978 | 0.920 | 0.96 | 1.007 | 1.0 | 0.980 | 0.932 | 1.084 | 0.900 |
| T-TS (21-20) | 1.043 | 1.026 | 1.01 | 1.006 | 1.07 | 0.990 | 0.957 | 0.995 | 1.0032 |
| T-TS (24-26) | 1.043 | 1.007 | 1.01 | 1.007 | 1.02 | 1.010 | 0.996 | 0.990 | 0.9879 |
| T-TS (7-29) | 0.967 | 0.907 | 0.97 | 0.975 | 0.97 | 0.990 | 0.963 | 0.996 | 0.9000 |
| T-TS (34-32) | 0.965 | 0.987 | 0.97 | 0.972 | 0.99 | 0.930 | 0.981 | 1.007 | 0.9802 |
| T-TS (11-41) | 0.955 | 0.901 | 0.9 | 0.900 | 0.9 | 0.910 | 1.062 | 0.990 | 0.9000 |
| T-TS (15-45) | 0.955 | 0.9 | 0.97 | 0.9718 | 0.96 | 0.9700 | 0.9755 | 0.9906 | 0.9000 |
| T-TS (14-46) | 0.900 | 0.9 | 0.95 | 0.953 | 0.95 | 0.9500 | 0.9639 | 1.0028 | 0.9000 |
| T-TS (10-51) | 0.930 | 0.916 | 0.96 | 0.9673 | 0.98 | 0.9800 | 0.9723 | 0.9900 | 0.9108 |
| T-TS (13-49) | 0.895 | 0.9 | 0.92 | 0.9278 | 0.93 | 0.9500 | 0.9248 | 1.0027 | 0.9000 |
| T-TS (11-43) | 0.958 | 0.9 | 0.96 | 0.964 | 0.99 | 0.9500 | 0.9554 | 1.0844 | 0.9000 |
| T-TS (40-56) | 0.958 | 0.998 | 1 | 0.9998 | 1.01 | 1.000 | 1.1000 | 1.0023 | 1.1024 |
| T-TS (39-57) | 0.980 | 0.994 | 0.96 | 0.9606 | 1.04 | 0.9600 | 0.9976 | 0.9900 | 0.9844 |
| T-TS (955) | 0.940 | 0.9 | 0.97 | 0.9789 | 0.96 | 0.9700 | 0.9845 | 1.0951 | 0.900 |
| QSC (18) | 0 | 4 | 9.984 | 9.9968 | 0.0442 | 0.0988 | 1.8917 | 4.9846 | 1.1581 |
| QSC (25) | 0 | 15 | 5.904 | 5.9000 | 0.0443 | 0.0542 | 5.2489 | 4.9992 | 4.9028 |
| QSC (53) | 0 | 11.67 | 6.288 | 6.300 | 0.0615 | 0.0628 | 5.1513 | 4.3653 | 4.7725 |
| Ploss (MW) | 27.86 | 26.68 | 24.26 | 24.252 | 24.593 | 24.89 | 24.752 | 22.918 | 21.6210 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wadood, A.; Ahmed, E.; Rhee, S.B.; Sattar Khan, B. A Fractional-Order Archimedean Spiral Moth–Flame Optimization Strategy to Solve Optimal Power Flows. Fractal Fract. 2024, 8, 225. https://doi.org/10.3390/fractalfract8040225
Wadood A, Ahmed E, Rhee SB, Sattar Khan B. A Fractional-Order Archimedean Spiral Moth–Flame Optimization Strategy to Solve Optimal Power Flows. Fractal and Fractional. 2024; 8(4):225. https://doi.org/10.3390/fractalfract8040225
Chicago/Turabian StyleWadood, Abdul, Ejaz Ahmed, Sang Bong Rhee, and Babar Sattar Khan. 2024. "A Fractional-Order Archimedean Spiral Moth–Flame Optimization Strategy to Solve Optimal Power Flows" Fractal and Fractional 8, no. 4: 225. https://doi.org/10.3390/fractalfract8040225
APA StyleWadood, A., Ahmed, E., Rhee, S. B., & Sattar Khan, B. (2024). A Fractional-Order Archimedean Spiral Moth–Flame Optimization Strategy to Solve Optimal Power Flows. Fractal and Fractional, 8(4), 225. https://doi.org/10.3390/fractalfract8040225







