Compact Trap-Assisted-Tunneling Model for Line Tunneling Field-Effect-Transistor Devices

Abstract

Trap-assisted-tunneling (TAT) is a well-documented source of severe subthreshold degradation in tunneling field-effect-transistors (TFET). However, the literature lacks in numerical or compact TAT models applied to TFET devices. This work presents a compact formulation of the Schenk TAT model that is used to fit experimental drain-source current (I_ds) versus gate-source voltage (V_gs) data of an L-shaped and line tunneling type TFET. The Schenk model incorporates material-dependent fundamental physical constants that play an important role in influencing the TAT generation (G_TAT) including the lattice relaxation energy, Huang–Rhys factor, and the electro-optical frequency. This makes fitting any experimental data using the Schenk model physically relevant. The compact formulation of the Schenk TAT model involved solving the potential profile in the TFET and using that potential profile to calculate G_TAT using the standard Schenk model. The G_TAT was then approximated by the Gaussian distribution function for compact implementation. The model was compared against technology computer-aided design (TCAD) results and was found in reasonable agreement. The model was also used to fit an experimental device’s I_ds–V_gs characteristics. The results, while not exactly fitting the experimental data, follow the general experimental I_ds–V_gs trend reasonably well; the subthreshold slope was loosely similar to the experimental device. Additionally, the ON-current, especially to make a high drain-source bias model accurate, can be further improved by including effects such as electrostatic degradation and series resistance.

1. Introduction

With conventional complementary metal-oxide-semiconductor (CMOS) technology coming to the end of its life cycle owing to scaling limitations, there has been significant interest in the research and development of alternate technologies including tunneling field-effect-transistors (TFET) [1,2,3]. TFETs work on the principle of band-to-band-tunneling, and provide a significantly better subthreshold slope (SS) as compared to metal-oxide-semiconductor field-effect-transistor (MOSFET) devices, and its ON-current (I_ON) issue [4] can be augmented with the help of alternate designs, including the line tunneling type TFET or III–V material TFET. In theory, this makes the TFET an ideal candidate to replace the aging MOSFET.

However, there is one issue that continues to be the bottleneck in the practical realization of the TFET. TFETs are very sensitive to subthreshold degradation caused by trap states [5]. Trap states cause trap-assisted-tunneling (TAT); TAT is a phonon-assisted band-to-band tunneling current generation process aided by trap states and is known to cause significant subthreshold slope degradation in TFETs. To date, there is very limited work available in the literature on the modeling of TAT mechanisms. Sajjad et al. [6] developed a compact TAT model based on Hurkx’s TAT model [7]. However, Hurkx’s TAT model can be considered a first-order model; it lacks fundamental and microscopic physical parameters that play a critical role in influencing TAT current including the phonon energy and Huang Rhys factor [8], which is a measure of the electron–phonon coupling and the lattice relaxation energy [9]. This makes fitting any experimental data with the help of the Hurkx model very difficult and without any physical relevance. Furthermore, the Hurkx model is a piece-wise model with different equations for different trap energy levels (E_T) [10]. This makes its compact implementation impractical. The Schenk model [11] on the other hand, offers a more microscopic approach to TAT modeling and is easy to implement numerically. The Schenk model has been used in studies investigating the role of TAT in TFET devices. However, there is no numerical or compact implementation of the Schenk model in the literature. This paper presents a simple Schenk–TAT compact model that is applied to fit the experimental drain–source current (I_ds)–gate–source voltage (V_gs) data of a line tunneling type and L-shaped TFET (LTFET) device [12]. The model is discussed in Section 2, and the results are discussed in Section 3. The conclusion is presented in Section 4.

2. Model Presentation

Figure 1a shows the schematic of the LTFET [12]. The channel is sandwiched between the gate and source. The source with height H_source = 70 nm is heavily p⁺ (10¹⁹ cm^-3) doped with H_source in the y direction, and the channel is n⁻ (10¹⁵ cm⁻³) doped. A part of the channel is also found underneath the source and does not overlap between the gate and source. This is termed as R_nonoverlap. The part of the channel that overlaps between the source and gate is termed as R_overlap and has a thickness T_j = 10 nm in the x direction and height (H_overlap = H_source = 70 nm [12,13]) in the y direction. The HfO₂ gate dielectric is 2 nm thick (t_ox). The drain is heavily n⁺ doped (10¹⁹ cm⁻³).

Before delving into the details of the model, it is important to illustrate the different current mechanisms in line tunneling TFETs. There are three different current mechanisms including (1) 2D BTBT, (2) 1D BTBT, and (3) TAT. 2D BTBTs originate from the corner-effect present in line tunneling TFETs. Because of the corner shape present in line tunneling TFETs, where the source and channel meet, the electric field converges around the sharp source corner, and increases the potential in the area surrounding the corner region [14]. This increased potential causes a 2D BTBT. The threshold voltage of 2D BTBT is lower than that of a 1D BTBT. However, the threshold voltage of the TAT is lower than that of the 2D BTBT and, as a consequence, the TAT current is generated at a lower V_gs than both the 2D and 1D BTBT currents. This is summarized in

Table 1. Current mechanisms in line tunneling TFETs and their threshold voltages.

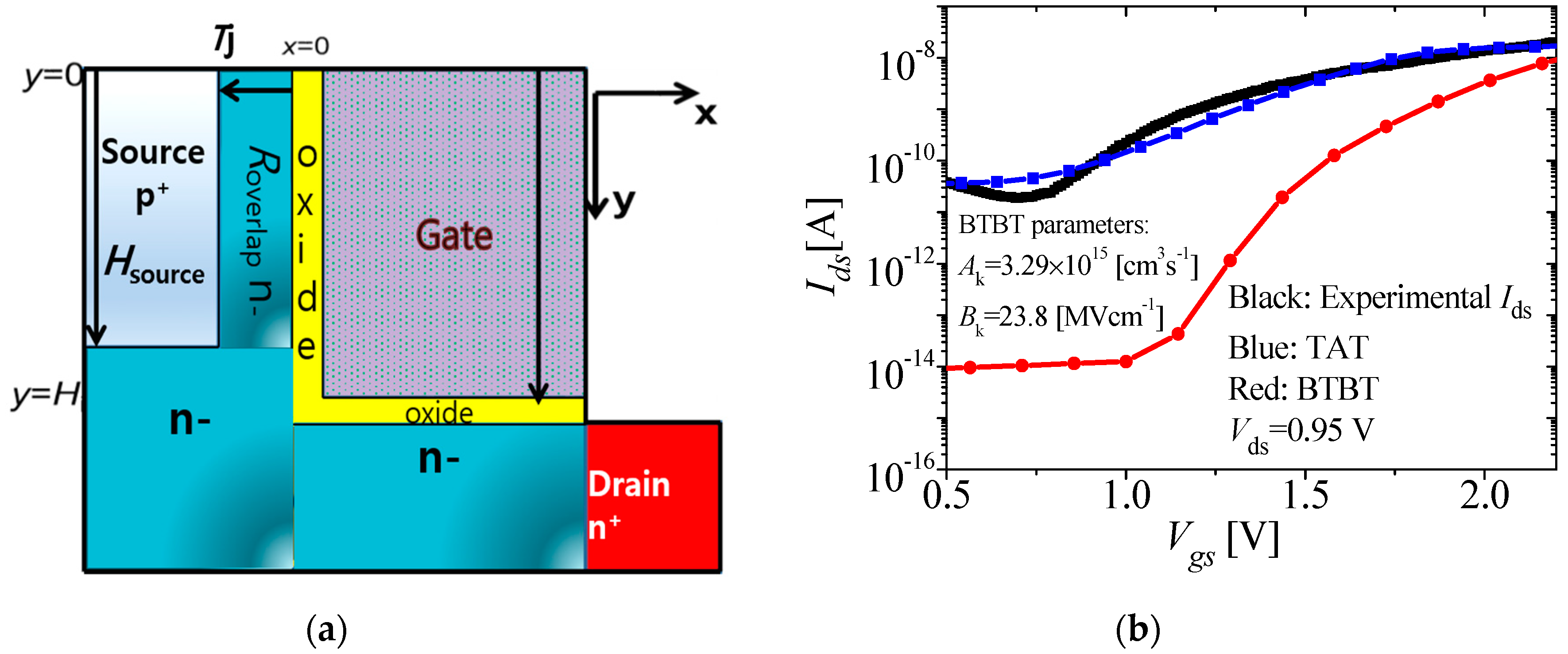
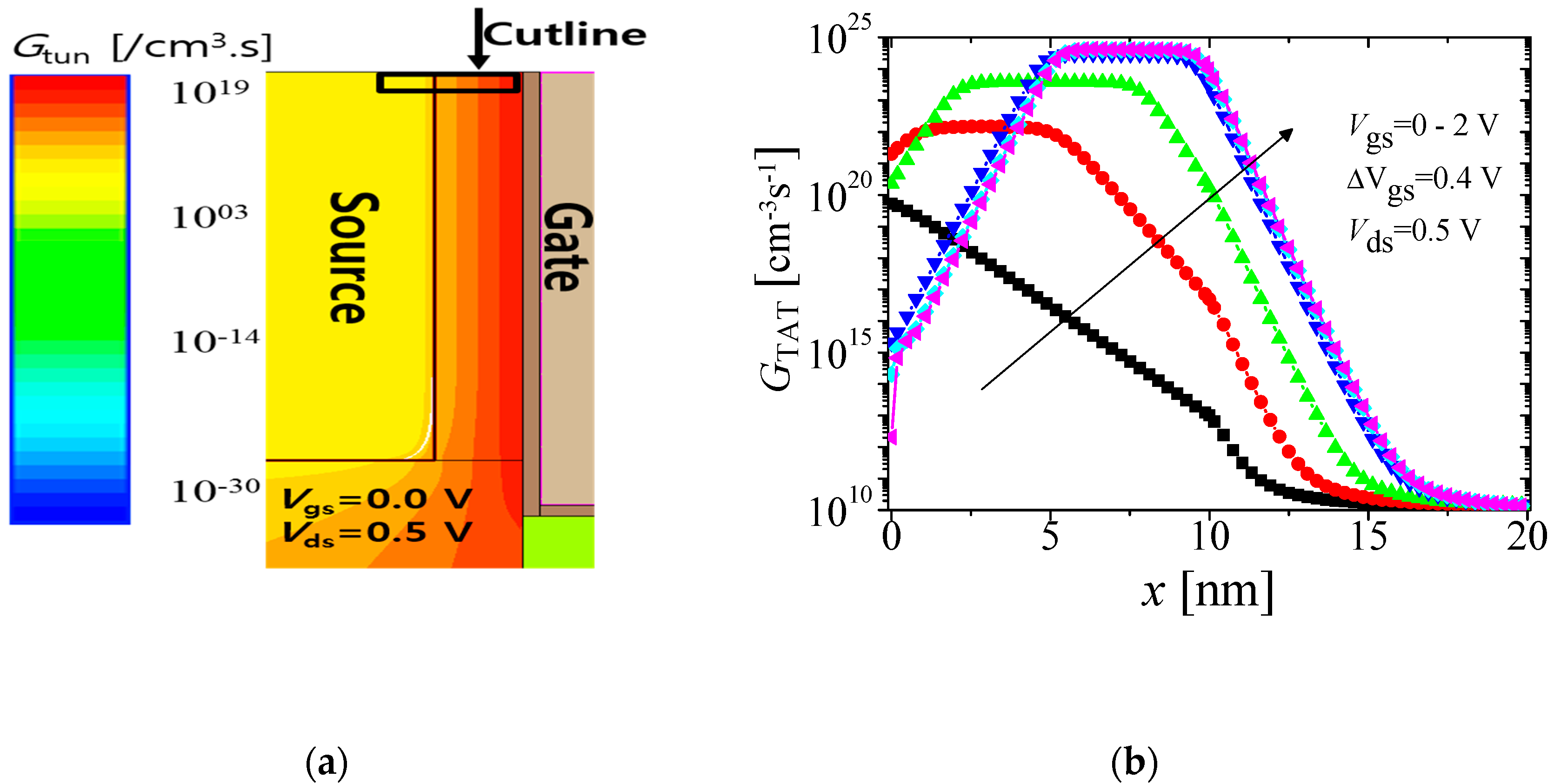
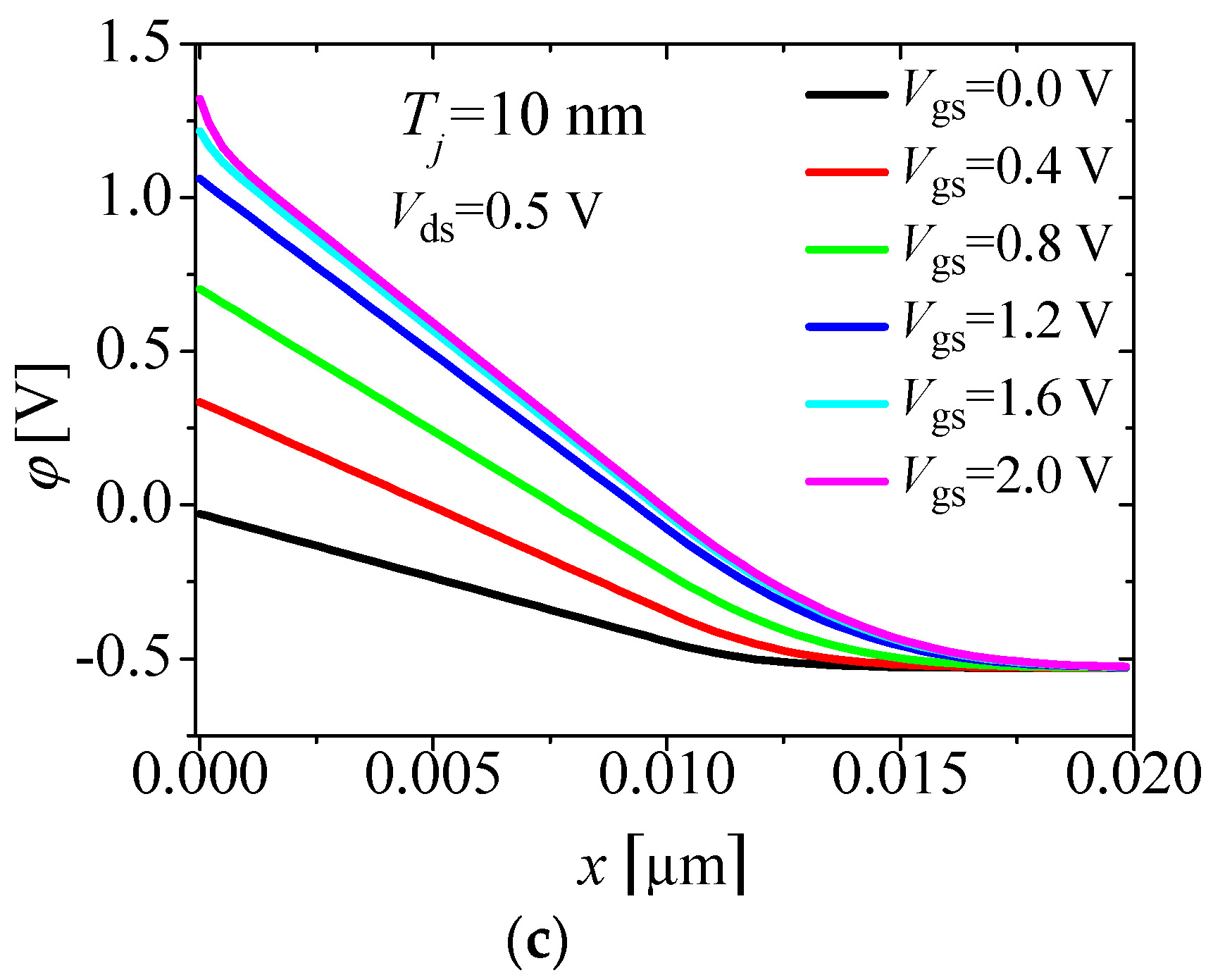
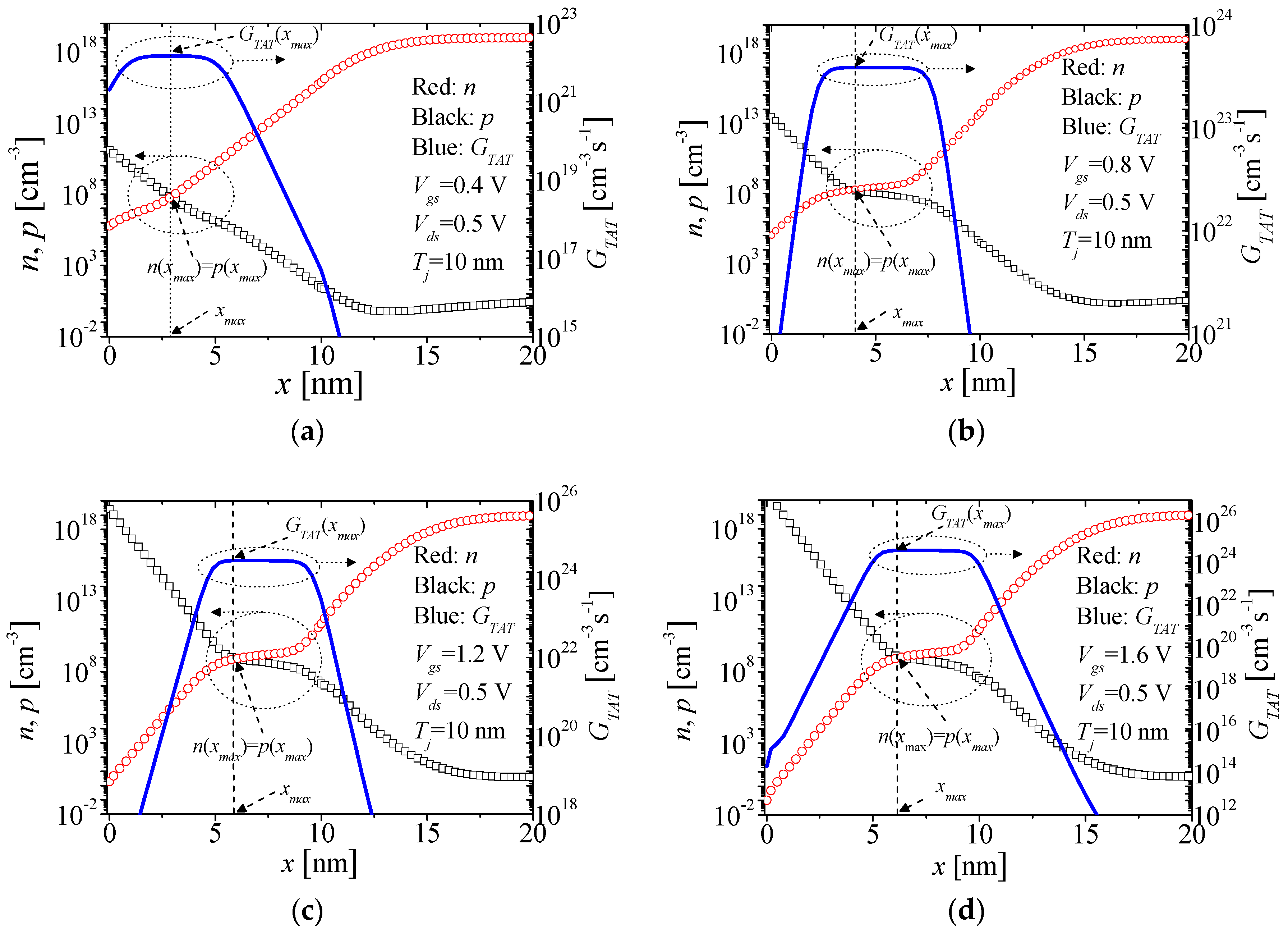
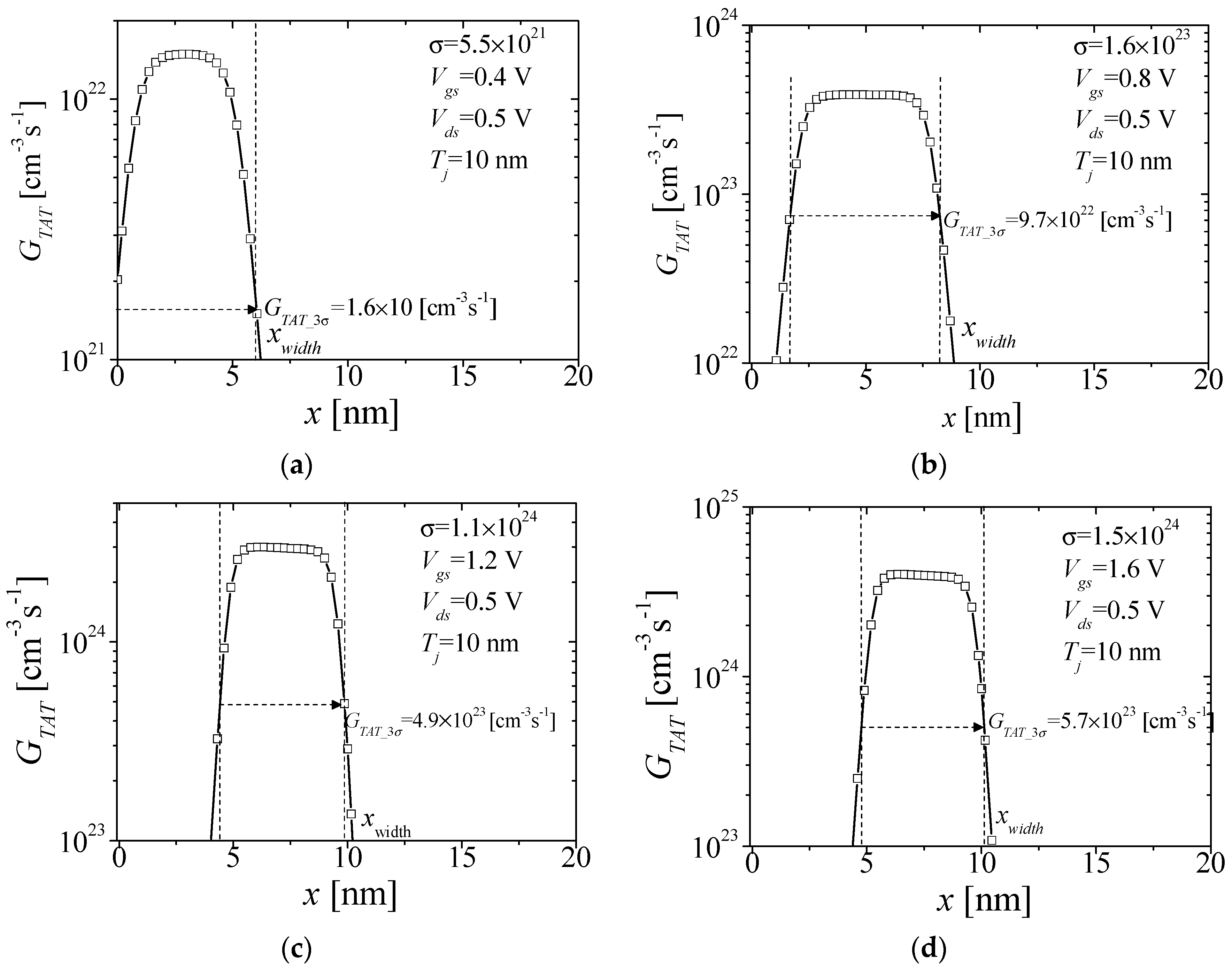
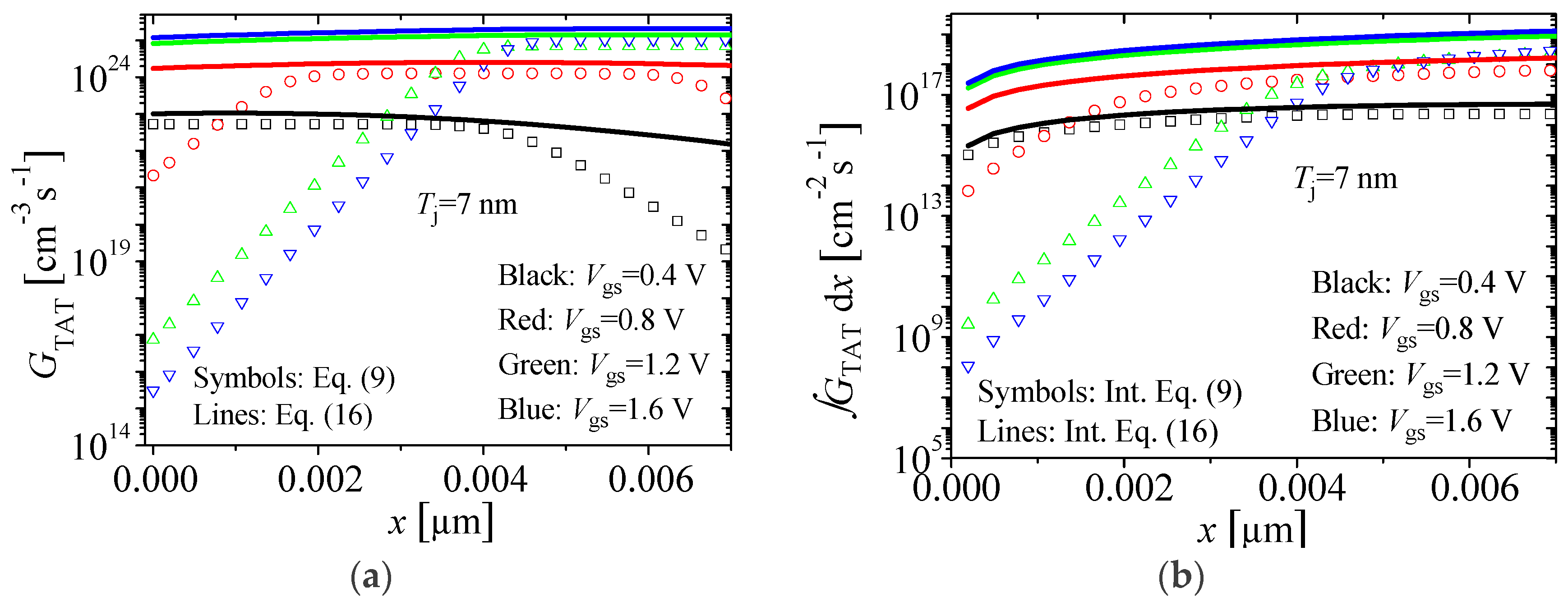
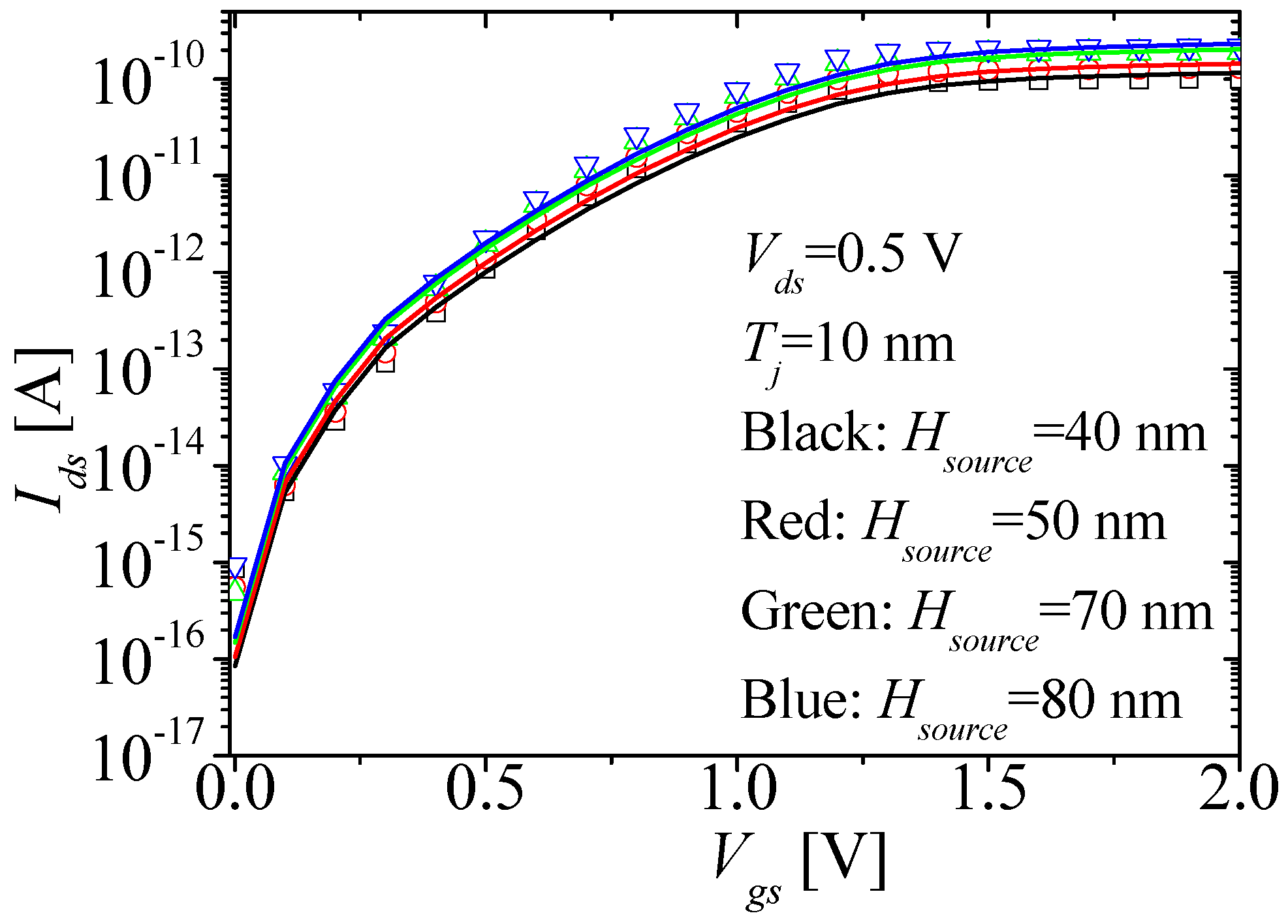
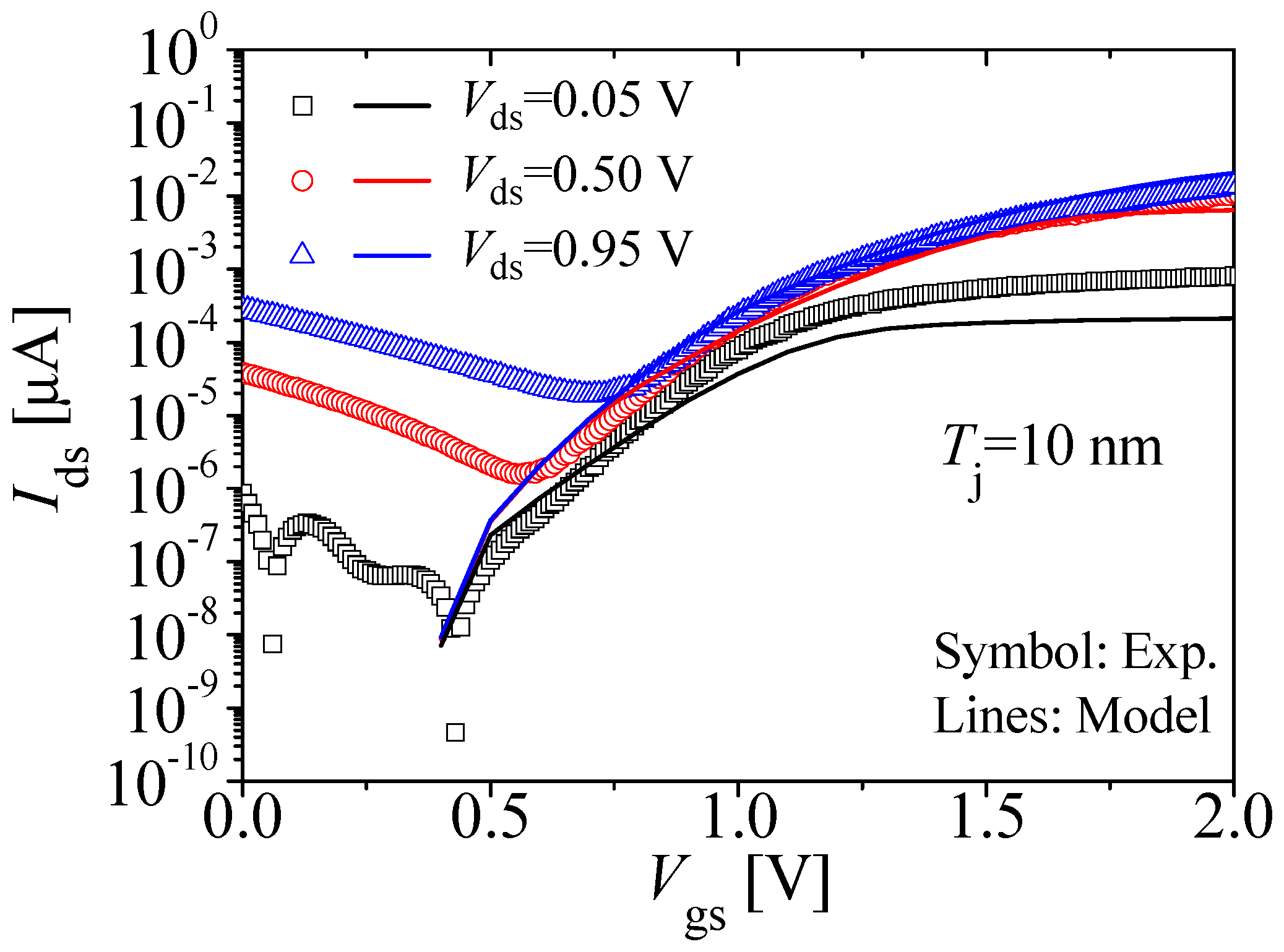
Mechanism	Region Dominated	Threshold Voltage
2D BTBT	Typically intermediate bias region.	TAT < 2D BTBT < 1D BTBT
1D BTBT	Typically subthreshold region.
TAT	Typically subthreshold and intermediate bias regions [5], and in extreme cases [13] the high bias region as well.

. Details of the 1D and 2D BTBT mechanisms can be found in [15,16]. Depending on the number of traps, their energy level, density and whether the traps are bulk or interface traps, the TAT generated drain current can vary. In most cases, the TAT current dominates the low V_gs bias subthreshold-BTBT current of TFETs [5,6], but in some cases such as the one reported in [13], the TAT current can dominate over the BTBT current for the entire V_gs range. This is explained with the help of Figure 1b. Figure 1b shows the I_ds-V_gs characteristics of the experimental LTFET [12]. It was first fitted using a dynamic nonlocal BTBT model [10] with theoretically determined, material-dependent A_k = 3.9 × 10¹⁵ cm³/s, and B_k = 23.8 MV/cm parameters. However, the BTBT–I_ds was found to be too low. With the BTBT current failing to match the experimental device’s I_ds, it was determined that it is instead the TAT-generated current that dominates for the entire V_gs range [13], as shown in Figure 1b.

For simplicity, only the 1D potential model is considered [15], and any 2D effects [16] are ignored. The model is divided into two parts. The first part deals with the potential model which has already been reported in detail in [16] and is only briefly described here. Next is the standard Schenk model itself, which has been taken from [10] followed by its compact implementation using the Gaussian distribution function.

2.1. Potential Model

Figure 2a shows the TAT generation rate (G_TAT) contour plot at V_gs = 0 V and V_ds = 0.5 V for an LTFET with T_j = 10 nm. Figure 2b shows the G_TAT extracted from the contour plot along the cutline indicated in Figure 2a, along with G_TAT at several V_gs biases ranging from 0 to 2 V. The region shown along the cutline is the reference region of the model, where all parameters including potential and G_TAT are calculated and assumed to be constant in the y and z directions. It can be seen that the G_TAT is significant only in the channel region, and for that reason, this model calculates G_TAT only in the channel region.

The potential model is based on solving the Poisson equation twice in the source and R_overlap regions. As a result, the potential and electric field (E) equations in the respective regions are given below [16].

Table 2. List of symbols specifically used in (1)–(7).

Symbol	Description	Value/Unit
φsource	Potential at source edge	V
Na, Nd	Source, channel doping	cm−3
xsource, xchannel	x co-ordinate in source, channel	cm
Ldep	Depletion length in source	cm
εsi, εox	Silicon, oxide permittivity	11.9Ɛ0, 25Ɛ0
Vfb,	Flat band voltage	V
q	Electron charge	1.6 × 10−19 C
φs,φj,φchannel	Surface potential at xchannel = 0, junction potential at x = Tj, and potential as a function of xchannel, respectively	V
φ;dep	Depletion potential in source	V
Cox	Gate capacitance	F/cm2
Vbis	Channel/source junction built-in potential	V

mentions the meaning of each symbol used in the following equations:

$$\frac{\partial {\phi }_{source}}{\partial x_{source}}=\frac{q{N}_a}{{\epsilon }_{si}}\left(x_{source}-L_{dep}\right)$$

(1)

$$\frac{\partial {\phi }_{channel}}{\partial x_{channel}}=-\frac{q{N}_d}{{\epsilon }_{si}}{x}_{channel}-\frac{{\epsilon }_{ox}}{{\epsilon }_{si}{t}_{ox}}\left(V_{gs}-V_{fb}-{\phi }_s\right)$$

(2)

$${\phi }_{source}\left(x_{source}\right)=\frac{q{N}_a}{2{\epsilon }_{si}}{\left(x_{source}-L_{dep}\right)}^2+{\phi }_{dep}$$

(3)

$${\phi }_{channel}\left(x_{channel}\right)=-\frac{q{N}_d}{2{\epsilon }_{si}}{x}_{channel}^2-\frac{{\epsilon }_{ox}}{{\epsilon }_{si}{t}_{ox}}\left(V_{gs}-V_{fb}-{\phi }_s\right)x_{channel}+{\phi }_s$$

(4)

$${\phi }_s=V_{gs}-V_{fb}+\frac{q\left(N_a+N_d\right)}{C_{ox}}{T}_j+\frac{q{\epsilon }_{si}{N}_a}{C_{ox}^2}-\gamma \sqrt{V_{gs}-V_{fb}+\frac{q\left(N_a+N_d\right)}{2{\epsilon }_{si}}{T}_j^2+\frac{q\left(N_a+N_d\right)}{C_{ox}}{T}_j+\frac{q{\epsilon }_{si}{N}_a}{2C_{ox}^2}-{\phi }_{dep}}$$

(5)

where $\gamma =\sqrt{2_{si}q{N}_d}/C_{ox}$_. The potential profile within the channel is assumed to be linear.

$${\phi }_{channel}\left(x_{channel}\right)=m{x}_{channel}+{\phi }_s$$

(6)

where m is the slope of the linear potential profile in the channel, m = (φ_s − φ_j)/T_j, or the electric field. Equation (6) is not derived from (2). It is a convenient assumption for compact modeling purposes. It can be seen in Figure 2c that potential follows a linear potential profile within the channel. Due to the strong band-bending, this assumption quasi-breaks down at higher V_gs bias. This consequence is explained later in Section 3. Because of the linear potential profile, E is constant throughout the channel and φ_j can be derived as

$${\phi }_j={\phi }_s+\frac{q{T}_j^2\left(N_d+2N_a\right)}{2{\epsilon }_{si}}-\sqrt{\frac{\left(2q{N}_a{T}_j^2\right)\left({\phi }_s+V_{bis}\right)}{{\epsilon }_{si}}+\frac{q^2{T}_j^4.\left(N_d{N}_a+N_a^2\right)}{{\epsilon }_{si}^2}}$$

(7)

2.2. Schenk Model

The Schenk model [7,10] works by modifying the lifetime parameter (τ₀) in the original Shockley–Read–Hall (SRH) recombination–generation model through the $\Gamma$ parameter as follows:

$${\tau }_{n\left(p\right)}=\frac{{\tau }_{0n\left(p\right)}}{1+{\Gamma }_{n\left(p\right)}\left(E\right)}$$

(8)

where n(p) in (8) represent electrons and holes, respectively. The Γ accounts for the E-driven, and phonon-assisted TAT process, and is calculated by the Schenk model. If there is any TAT present, Γ is usually significantly higher than 1 [5]. Otherwise, it is zero. The lifetime given by (8) features in the SRH model expression, which is used to give G_TAT if Γ > 0, as follows:

$$G_{TAT}=\frac{np-n_i^2}{\frac{{\tau }_{0p}}{1+{\Gamma }_p}\left(n+n_1\right)+\frac{{\tau }_{0n}}{1+{\Gamma }_n}\left(p+p_1\right)}$$

(9)

where n_i is an intrinsic carrier concentration, $n_1=n_{i}exp\left(E_T/kT\right)$, $p_1=n_{i}exp\left(E_T/kT\right)$, and k and T are the Boltzmann constant and temperature, respectively. n and p in (9) are given by

$$n=n_i.exp\left(\frac{\phi \left(x\right)-{\phi }_{equasi}}{v_{th}}\right), p=n_i.exp\left(-\frac{\phi \left(x\right)}{v_{th}}\right)$$

(10)

where v_th and φ_equasi present thermal voltage and electron quasi Fermi level, respectively. Substituting for φ_channel from (6) in (10), n and p are given by

$$n\left(x\right)=n_i.exp\left(\frac{mx+{\phi }_s-{\phi }_{quasi}}{v_{th}}\right), p\left(x\right)=n_i.exp\left(-\frac{mx+{\phi }_s}{v_{th}}\right).$$

(11)

Γ is calculated by the following equation. A detailed derivation of this equation is given in [7].

$${\Gamma }_{n\left(p\right)}={\left(1+\frac{{\left(ħ{\Theta }_{n\left(p\right)}\right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\sqrt{E_{tn\left(p\right)}-E_{0n\left(p\right)}}}{E_{0n\left(p\right)}ħ{\omega }_0}\right)}^{-\frac{1}{2}}\frac{{\left(ħ{\Theta }_{n\left(p\right)}\right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}{\left(E_{tn\left(p\right)}-E_{0n\left(p\right)}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}}{2\sqrt{E_{tn\left(p\right)}{E}_{0n\left(p\right)}}}{\left(\frac{ħ{\Theta }_{n\left(p\right)}}{kT}\right)}^{\frac{3}{2}}·exp\left(-\frac{E_{tn\left(p\right)}-E_{0n\left(p\right)}}{ħ{\omega }_0}+\frac{ħ{\omega }_0-kT}{2ħ{\omega }_0}+\frac{2E_{tn\left(p\right)}+kT}{2ħ{\omega }_0}\ln \frac{E_{tn\left(p\right)}}{{\epsilon }_R}-\frac{E_{0n\left(p\right)}}{ħ{\omega }_0}\ln \frac{E_{0n\left(p\right)}}{{\epsilon }_R}+\frac{E_{tn\left(p\right)}-E_{0n\left(p\right)}}{kT}-\frac{4}{3}{\left(\frac{E_{tn\left(p\right)}-E_{0n\left(p\right)}}{ħ{\Theta }_{n\left(p\right)}}\right)}^{\frac{3}{2}}\right).$$

(12)

Here, ħ is the reduced Planck’s constant, ħω₀ is the effective phonon energy (E_phon), ε_R = SE_phon is the lattice relaxation energy [17] which is known to influence the subthreshold slope (SS), where S is the Huang–Rhys factor [18] which is a measure of electron–phonon coupling. Both E_phon and S are known to influence Γ, although the effect of E_phon has been found to be dominant over S on Γ. Furthermore, the current can change if either S or E_phon change, even if ε_R remains constant [18]. E_tn(p) is the energy at which the tunneling probability for the carriers to the tunnel from E_T to the band edge is the maximum and ${\Theta }_{n\left(p\right)}=$(q²E²/2ħm_n(p))^1/3 is the electro-optical frequency [18]. m_n and m_p are the electron and hole tunneling masses, respectively.

The model parameters including trap level E_T, S, E_phon, and ${}_{n\left(p\right)}$ are the fundamental quantities that strongly influence the TAT process. The first three can be determined experimentally using Deep Level Transient Spectroscopy [19,20]. The electro-optical frequency is dependent on the electric field and the tunneling masses. This restricts the model to being a local TAT model [18]. E_0n(p) is the energy of an optimum horizontal transition path which is dependent on the field strength and temperature. This determines the most probable recombination path [18], and is given by

$$E_{0n\left(p\right)}=2\sqrt{{\epsilon }_{Fn\left(p\right)}}\left[\sqrt{{\epsilon }_{Fn\left(p\right)}+E_{tn\left(p\right)}+{\epsilon }_R}-\sqrt{{\epsilon }_{Fn\left(p\right)}}\right]-{\epsilon }_R$$

(13)

where ${\epsilon }_{Fn\left(p\right)}=\frac{{\left(2{\epsilon }_{F}kT\right)}^2}{{\left(ħ{\Theta }_{n\left(p\right)}\right)}^3}$. E_tn for electrons is given by

$$E_{tn}=\frac{1}{2}{E}_{bgn}+\frac{3}{4}kT\ln \left(\frac{m_n}{m_p}\right)-E_T-{\left(32R_c{ħ}^3{\Theta }^3\right)}^{\frac{1}{4}}$$

(14)

and E_tp is given by

$$E_{tp}=\frac{1}{2}{E}_{bgn}+\frac{3}{4}kT\ln \left(\frac{m_n}{m_p}\right)-E_T+{\left(32R_v{ħ}^3{\Theta }^3\right)}^{\frac{1}{4}}$$

(15)

where R_c(v) are the effective Rydberg energies; R_c(v) = m_n(p)R_y/ε² for electrons (holes), where R_y (= 13.6 eV) is the Rydberg energy and ε is the permittivity.

2.3. Compact Implementation

For compact implementation, G_TAT given by (9) is approximated using a Gaussian distribution function as follows:

$$G_{TAT}=G_{TAT\_max}exp\left(-{\left(\frac{x-x_{max}}{x_{width }}\right)}^2\right)$$

(16)

where x_width is the width of the Gaussian distribution. G_{TAT_max} is the maximum G_TAT along the channel region, and x_max is the x-point where G_TAT is maximum. G_{TAT_max} always occurs where n = p. This can be seen in Figure 3 which shows n, p (left axis), and G_TAT (right axis) at different V_gss for V_ds=0.5 V, for an LTFET with T_j = 10 nm. It can be seen from Figure 3 that at the point where n = p, G_TAT is maximum. The x co-ordinate where this occurs is labelled as x_max. x_max can be found by equating n = p, as follows: and solving for x, that is.

$$n_{i}exp\left(\frac{m{x}_{max}+{\phi }_s-{\phi }_{equasi}}{v_{th}}\right)=n_{i}exp\left(-\frac{m{x}_{max}+{\phi }_s}{v_{th}}\right)$$

(17)

$$x_{max}=\frac{{\phi }_{equasi}-\left(2{\phi }_s\right)}{2m}$$

(18)

G_{TAT_max} is found by using x_max in (9), as follows:

$$G_{TAT\_max}=\frac{n(x_{max})p(x_{max})-n_i^2}{\frac{{\tau }_{0p}}{1+{\Gamma }_p}\left[n(x_{max})+n_1\right]+\frac{{\tau }_{0n}}{1+{\Gamma }_n}\left[p(x_{max})+p_1\right]}$$

(19)

where n(x_max) and p(x_max) can be found using x = x_max in (11). It should be mentioned that Γ is independent of x; constant electric field in the channel makes Γ calculated from (12) essentially independent of x. In order to find x_width, the standard deviation (σ) of the Gaussian distribution is utilized. σ is obtained using standard equations [21]. Utilizing the Empirical Rule in Statistics and Probability [21] which states that 99.7% of values in a normal distribution lie within 3 standard deviations of the mean value [21], the width of Gaussian distribution was approximated at 3 standard deviations of the maximum value of the function, that is, the width was estimated to be the x co-ordinate (x_width) that satisfied this condition, $3\sigma of G_{TAT}$, symbolized by $G_{TAT\_3\sigma }$. Substituting this condition in (9), along with (11), assuming mid-gap trap level so that n₁ = p₁ = n_i, (9) can be given by

$$G_{TAT\_3\sigma }=\frac{n_i^{2}exp\left(\frac{-{\phi }_{quasi}}{v_{th}}\right)-n_i^2}{\frac{{\tau }_{0p}}{1+{\Gamma }_p}\left(n+n_i\right)+\frac{{\tau }_{0n}}{1+{\Gamma }_n}\left(p+n_i\right)}$$

(20)

It can be seen from Figure 3 and Figure 4 that at any bias, the width of the Gaussian distribution n >> p. Furthermore, assuming equivalent τ_0n = τ_0p = τ₀, and Γ_n~Γ_p which is true for the materials with m_e~m_p including silicon, and advanced III-V InGaAs-based materials [13], (20) can be expressed as

$$G_{TAT\_3\sigma }=\frac{n_i^{2}exp\left(\frac{-{\phi }_{quasi}}{v_{th}}\right)-n_i^2}{\frac{{\tau }_0}{1+{\Gamma }_n}\left[n_i\left(exp \left(\frac{m{x}_{width}+{\phi }_s-{\phi }_{quasi}}{v_{th}}\right)+2\right)\right]}$$

(21)

Taking log on both sides, ignoring 2, and solving for x_width, x_width can be given by

$$x_{width}=\frac{\left\{\log \left[\left(G_{TAT\_3\sigma }\right)\left(\frac{{\tau }_0}{1+{\Gamma }_n}\right)\right]-\log \left(n_i\right)\right\}.\left(v_{th}-{\phi }_s\right)}{m}$$

(22)

The TAT drain current (I_{ds_TAT}) is given by the following expression:

$$I_{ds\_TAT}=q{{\displaystyle \int }}_0^{abs\left(T_j\right)}{{\displaystyle \int }}_0^{H_{source}}{{\displaystyle \int }}_0^W{G}_{TAT}dxdydz=qW{H}_{source}{{\displaystyle \int }}_0^{abs\left(T_j\right)}{G}_{TAT}dx$$

(23)

$$I_{ds\_TAT}=\sqrt{\pi }qW{H}_{source}{G}_{TAT\_Max}{x}_{width}\left[erf\left(\frac{abs\left(T_j\right)-x_{\max }}{x_{width}}\right)-erf\left(\frac{0-x_{max}}{x_{width}}\right)\right]$$

(24)

where W is the width of the device. It is assumed that G_TAT is independent of H_source, and W. Note that (24) is simply the closed-integral expression of (16) integrated between T_j and 0 μm at the surface.

3. Results

To demonstrate whether the Gaussian approximation of G_TAT is feasible, Figure 5 compares G_TAT calculated from the actual SRH-based G_TAT equation: (9) and G_TAT approximated by Gaussian approximation: (16) for T_j = 7 nm. The approximated G_TAT is reasonably consistent with the calculated G_TAT. It should be emphasized that this is only an approximation for compact modeling purposes. The approximated G_TAT overestimates the actual G_TAT, particularly at high bias values. The overestimation at higher V_gs bias is because the linear potential profile assumption does not remain valid at high V_gs bias. Figure 5b shows two integrated G_TAT. Based on Figure 5a,b, some overestimation of I_{ds_TAT} can be expected at high V_gs bias.

Figure 6 compares I_{ds_TAT} from the technology computer-aided design (TCAD) (symbol) against I_{ds_TAT} calculated from (24) for different T_j. Considering that this is a compact model, a reasonable agreement on the simulation results between the TCAD and the model is observed. The expected overestimation in I_{ds_TAT} at high V_gs bias can be seen in Figure 6. Figure 7 compares I_{ds_TAT} from the TCAD (symbols) against I_{ds_TAT} calculated from the model for T_j = 10 nm and different H_source, at V_ds = 0.5 V. The slight disagreement at higher bias is due to the linear potential approximation which is not very accurate at higher bias due to strong surface band bending.

To truly test the relevancy of the model, the model was used to fit experimental data from [12]. It was found in [13] that I_{ds_TAT} dominates the entire V_gs range for all V_ds biases. Therefore, I_{ds_TAT} from the model was compared against the experimental data. The result is shown in Figure 8. The model was calibrated to match the experimental I_ds–V_gs characteristics at V_ds = 0.95 V by choosing τ₀ = 10⁻¹¹ s. The model follows the experimental I_ds trend very well. However, it is not entirely accurate, especially at low V_ds. The reason for this is that (1) the electrostatic degradation caused by the trap states was not considered in this work. Electrostatic degradation causes the potential to degrade, and this effect becomes more important at high bias. To account for that, the Poisson and trap charge need to be calculated self-consistently. Furthermore, a different potential profile expression other than the linear potential profile given by (6) will be needed. This is because with the traps causing electrostatic degradation, the degraded potential profile changes from being linear to non-linear. It should be emphasized that from Figure 1b, BTBT current calculated using experimentally determined A_k/B_k parameters was found to be too low than the current of the experimental device. The absence of BTBT current in this particular example is not the result of mismatch. An ambipolar current was also found to be a factor in the experimental device which could be important at low V_gs bias. The other reasons possibly include the use of abrupt doping profiles, and abrupt geometry in the simulation. The limitations of the model include the use of one trap at the mid-gap level, and the lack of electrostatic degradation.

4. Conclusions

The literature lacks a compact tunable trap-assisted-tunneling model. This work presented a compact TAT model that captured important physical parameters that influence the TAT process including phonon energy, the Huang–Rhys factor, and tunneling masses. The model is divided into three parts. The first part includes the potential model, the second part includes the standard Schenk model equations, and the third part includes the compact implementation of the Schenk model where the TAT tunneling rate is expressed as a Gaussian distribution. The approximated Gaussian distribution is then integrated along the x-axis to generate a TAT-generated drain current. The model was tested against the TCAD data and was found to be in reasonable agreement. The model was also tested against I_ds from an experimental device. The model was found to follow the same trend as the experimental device. The result, however, was not truly accurate. This could be due to neglecting the electrostatic degradation caused by the traps which could be important at high bias. Another reason for the inaccuracy could be neglecting effects such as contact resistance in the model. In summary, this work provides a useful contribution within the compact trap-assisted-tunneling modeling domain of TFET devices. The compact implementation part of the model can be generalized for use in any TFET device and can easily be incorporated in the simulation program with integrated circuit emphasis (SPICE) framework. For the completed compact model of the TET for SPICE implementation, series resistance [22], SRH [23], ambipolar, quantum confinement [24], and breakdown models [25] should be added to this proposed model.