Compact Trap-Assisted-Tunneling Model for Line Tunneling Field-Effect-Transistor Devices
Abstract
:1. Introduction
2. Model Presentation
2.1. Potential Model
2.2. Schenk Model
2.3. Compact Implementation
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Boucart, K.; Ionescu, A. Double-gate tunnel FET with high-κ gate dielectric. IEEE Trans. Electron. Devices 2007, 54, 1725–1733. [Google Scholar] [CrossRef]
- Flori, G.; Iannaccone, G. Ultra-voltage bilayer graphene tunnel FET. IEEE Electron. Device Lett. 2009, 30, 1096–1098. [Google Scholar]
- Datta, S.; Liu, H.; Narayan, V. Tunnel FET Technology: A Reliability Perspective. Microelectron. Reliab. 2014, 54, 861–874. [Google Scholar] [CrossRef]
- Alian, A.; Mols, Y.; Bordallo, C.C.M.; Verreck, D.; Verhulst, A.; Vandooren, A.; Rooyackers, R.; Agopian, P.G.D.; Martino, J.A.; Thean, A.; et al. InGaAs tunnel FET with sub-nanometer EOT and sub-60 mV/dec sub-threshold swing at room temperature. Appl. Phys. Lett. 2016, 109, 243502. [Google Scholar] [CrossRef] [Green Version]
- Sajjad, R.N.; Chern, W.; Hoyt, J.L.; Antoniadis, D.A. Trap assisted tunneling and its effect on subthreshold swing of tunnel FETs. IEEE Trans. Electron. Devices 2016, 63, 4380–4387. [Google Scholar] [CrossRef]
- Sajjad, R.N.; Antoniadis, D. A compact model for tunnel FET for all operating regimes including trap assisted tunneling. In Proceedings of the 2016 74th Annual Device Research Conference (DRC), Newark, DE, USA, 19–22 June 2016. [Google Scholar]
- Hurkx, G.A.M.; Klassen, D.B.M.; Knuvers, M.P.G. A new recombination model for device simulation including tunneling. IEEE Trans. Electron. Devices 1992, 39, 331–338. [Google Scholar] [CrossRef]
- Jiménez-Molinos, F.; Palma, A.; Gámiz, F.; Banqueri, J.; López-Villanueva, J.A. Physical model for trap-assisted inelastic tunneling in metal-oxide-semiconductor structures. J. Appl. Phys. 2001, 90, 3396–3404. [Google Scholar] [CrossRef]
- Schenk, A.; Sant, S.; Moselund, K.; Riel, H. The impact of hetero-junction and oxide-interface traps on the performance of InAs/Si tunnel FETs. In Proceedings of the 2017 17th International Workshop on Junction Technology, Uji, Japan, 1–2 June 2017. [Google Scholar]
- Synopsys. User Manual, Version L-2016.03, Synopsys TCAD Sentaurus; Synopsys: San Jose, CA, USA, 2016. [Google Scholar]
- Schenk, A. A model for the field and temperature dependence of Shockley–Read–Hall lifetimes in silicon. Solid-State Electron. 1992, 35, 1585–1596. [Google Scholar] [CrossRef]
- Kim, S.W.; Kim, J.H.; Liu, T.K.; Choi, W.Y.; Park, B. Demonstration of L-shaped tunnel field-effect transistors. IEEE Trans. Electron. Devices 2016, 63, 1774–1778. [Google Scholar] [CrossRef]
- Najam, F.; Yu, Y.S. Physically consistent method for calculating trap-assisted-tunneling current applied to line tunneling field-effect-transistor. IEEE Trans Electron. Devices 2020, 67, 2106–2112. [Google Scholar] [CrossRef]
- Vandenberghe, W.G.; Verhulst, A.S.; Groeseneken, G.; Soree, B.; Magnus, W. Analytical model for point and line tunneling in a tunnel field-effect transistor. In Proceedings of the 2008 International Conference on Simulation of Semiconductors Processes and Devices, Hakone, Japan, 9–11 September 2008. [Google Scholar]
- Najam, F.; Yu, Y.S. Investigation of corner effect and identification of tunneling regimes in L-shaped tunnel field-effect-transistor. J. Nanosci. Nanotechnol. 2018, 18, 6578–6583. [Google Scholar] [CrossRef] [PubMed]
- Najam, F.; Yu, Y.S. Compact model for L-shaped tunnel field-effect transistor including the 2D region. Appl. Sci. 2019, 9, 3716. [Google Scholar] [CrossRef] [Green Version]
- Smets, Q.; Verhulst, A.S.; Simeon, E.; Gundlach, D.; Richter, D.; Collaert, N.; Heyns, M.M. Calibration of bulk trap-assisted tunneling and Shockley–Read–Hall currents and impact on InGaAs tunnel-FETs. IEEE Trans. Electron. Devices 2017, 64, 3622–3626. [Google Scholar] [CrossRef]
- Mandurrino, M.; Goano, M.; Vallone, M.; Bertazzi, F.; Ghione, G.; Verzellesi, G.; Meneghini, M.; Meneghesso, G.; Zanoni, E. Semiclassical simulation of trap-assisted tunneling in GaN-based light-emitting diodes. J. Comput. Electron. 2015, 14, 444–445. [Google Scholar] [CrossRef]
- Vincent, G.; Chantre, A.; Bois, D. Electric field effect on the thermal emission of traps in semiconductor junctions. J. Appl. Phys. 1972, 50, 5484–5487. [Google Scholar] [CrossRef]
- Fleming, R.M.; Seager, C.H.; Lang, D.V.; Campbell, J.M. Injection deep level transient spectroscopy: An improved method for measuring capture rates of hot carriers in semiconductors. J. Appl. Phys 2015, 118, 015703. [Google Scholar] [CrossRef]
- Mendenhall, W.; Beaver, R.J.; Beaver, B.M. Introduction to Probability and Statistics Metric Edition, 15th ed.; Cengage Learning US: Boston, MA, USA, 2019. [Google Scholar]
- Klassen, F.; Biermans, P.; Velghe, R. The series resistance of submicron MOSFETs and its effect on their characteristics. J. Phys. Colloq. 1988, 49, C4-257–C4-260. [Google Scholar] [CrossRef]
- Liu, Y.; Yan, J.; Wang, H.; Han, G. Temperature dependent IDS–VGS characteristics of an N-channel Si tunneling field-effect transistor with a germanium source on Si(110) substrate. J. Semicond. 2014, 35, 024001. [Google Scholar] [CrossRef]
- Walke, A.M.; Verhulst, A.S.; Vandooren, A.; Verreck, D.; Simoen, E.; Rao, V.R.; Groeseneken, G.; Collaert, N.; Thean, A.V.Y. Part I: Impact of field-induced quantum confinement on the subthreshold swing behavior of line TFETs. IEEE Trans. Electron. Devices 2013, 60, 4057–4064. [Google Scholar] [CrossRef]
- Jung, H.; Dimitrijev, S. Analysis of flat-band-voltage dependent breakdown voltage for 10 nm double gate. MOSFET. J. Inf. Commun. Converg. Eng. 2018, 16, 43–47. [Google Scholar]
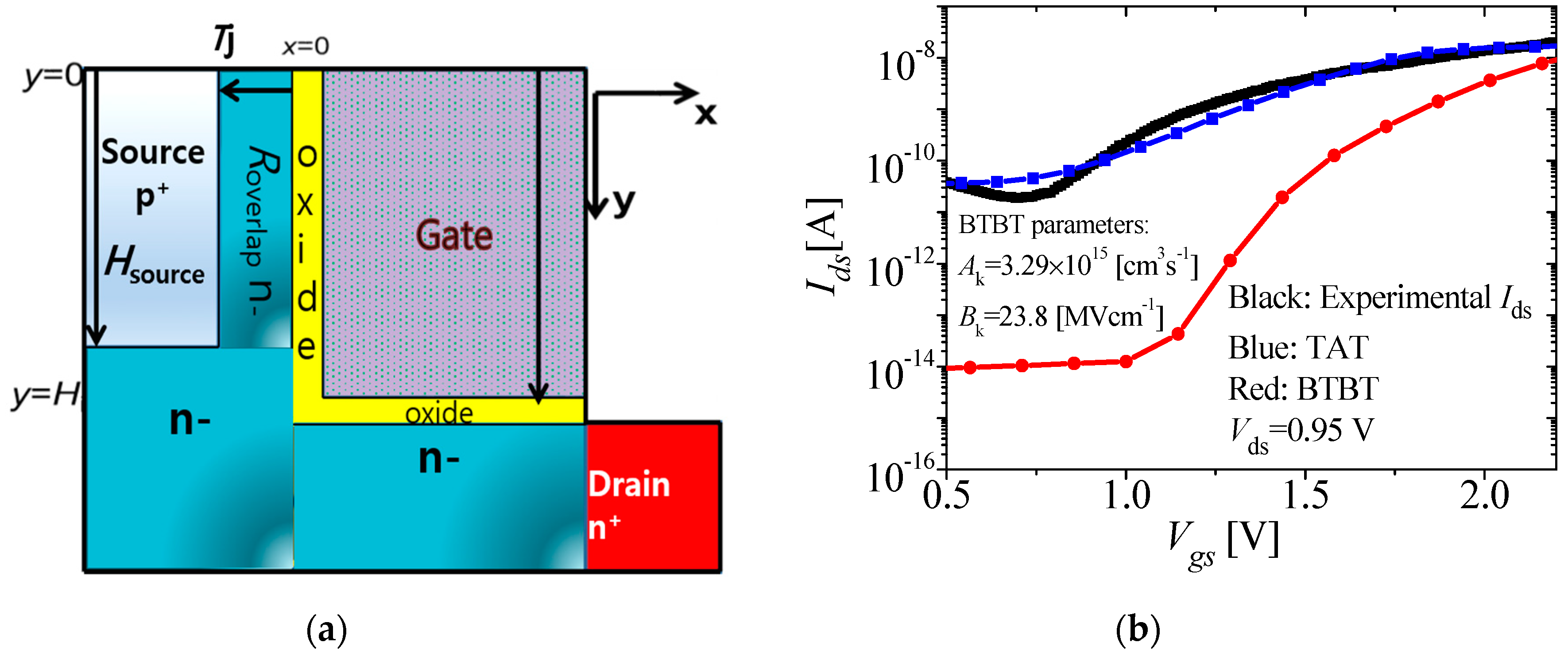
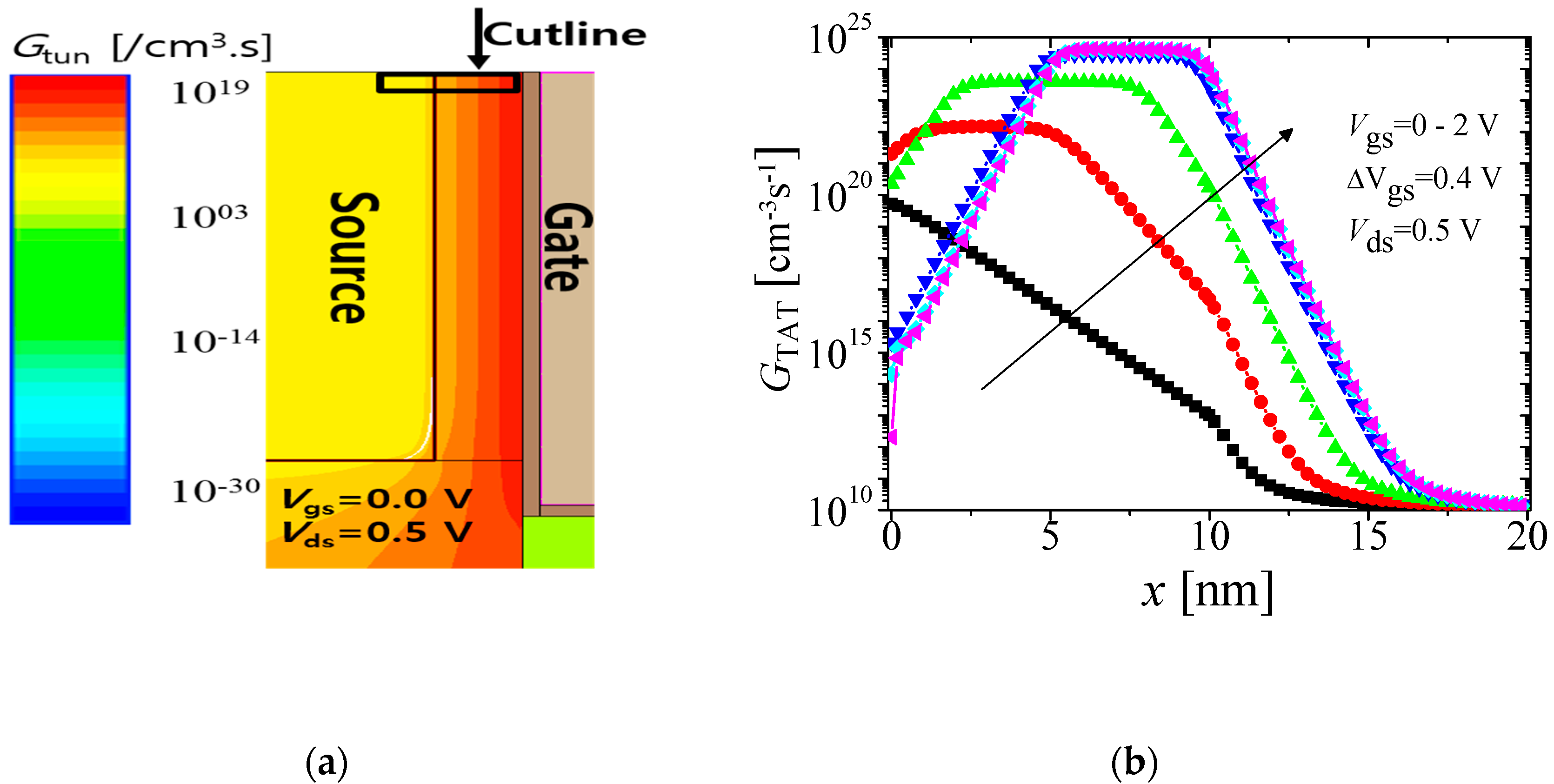
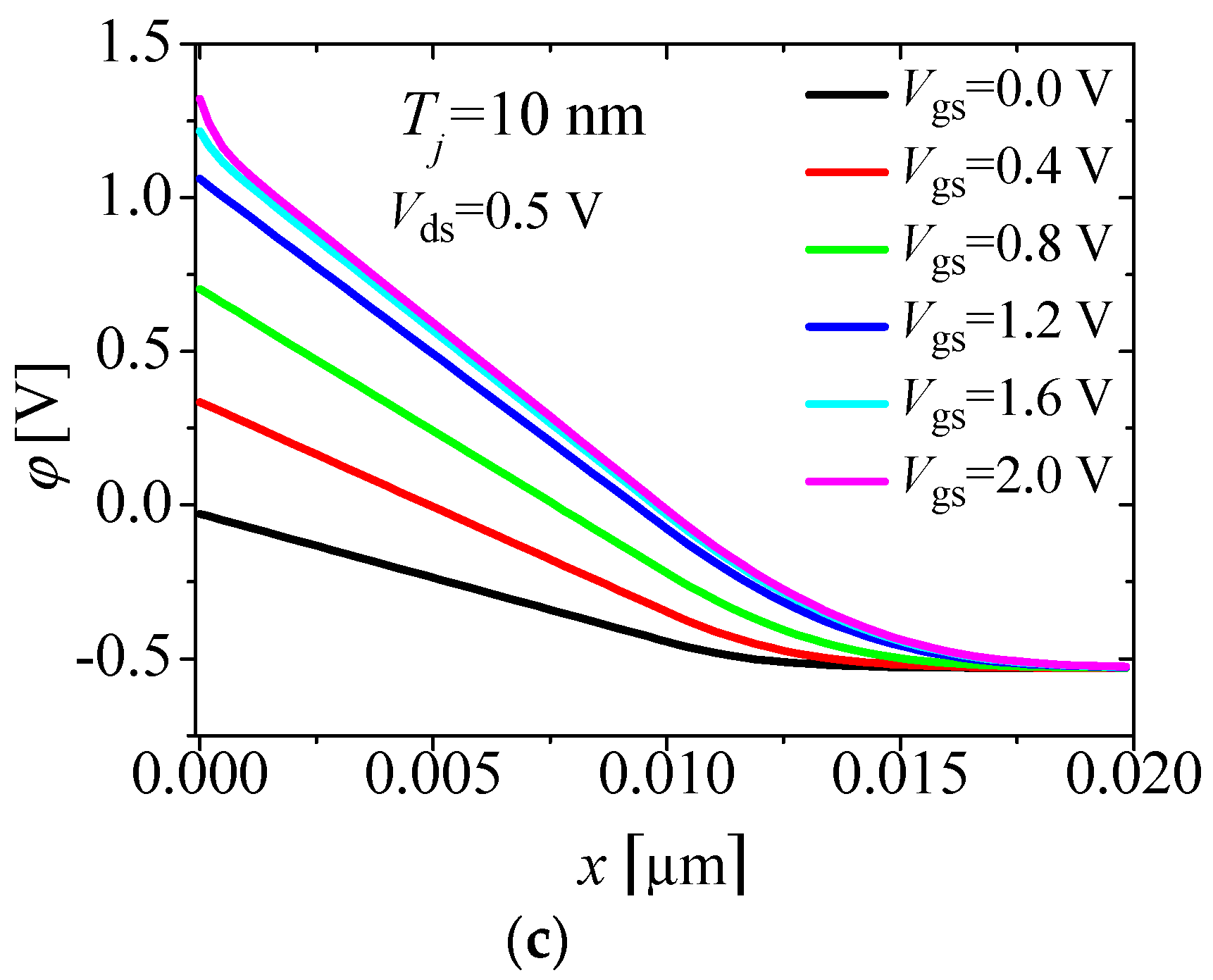
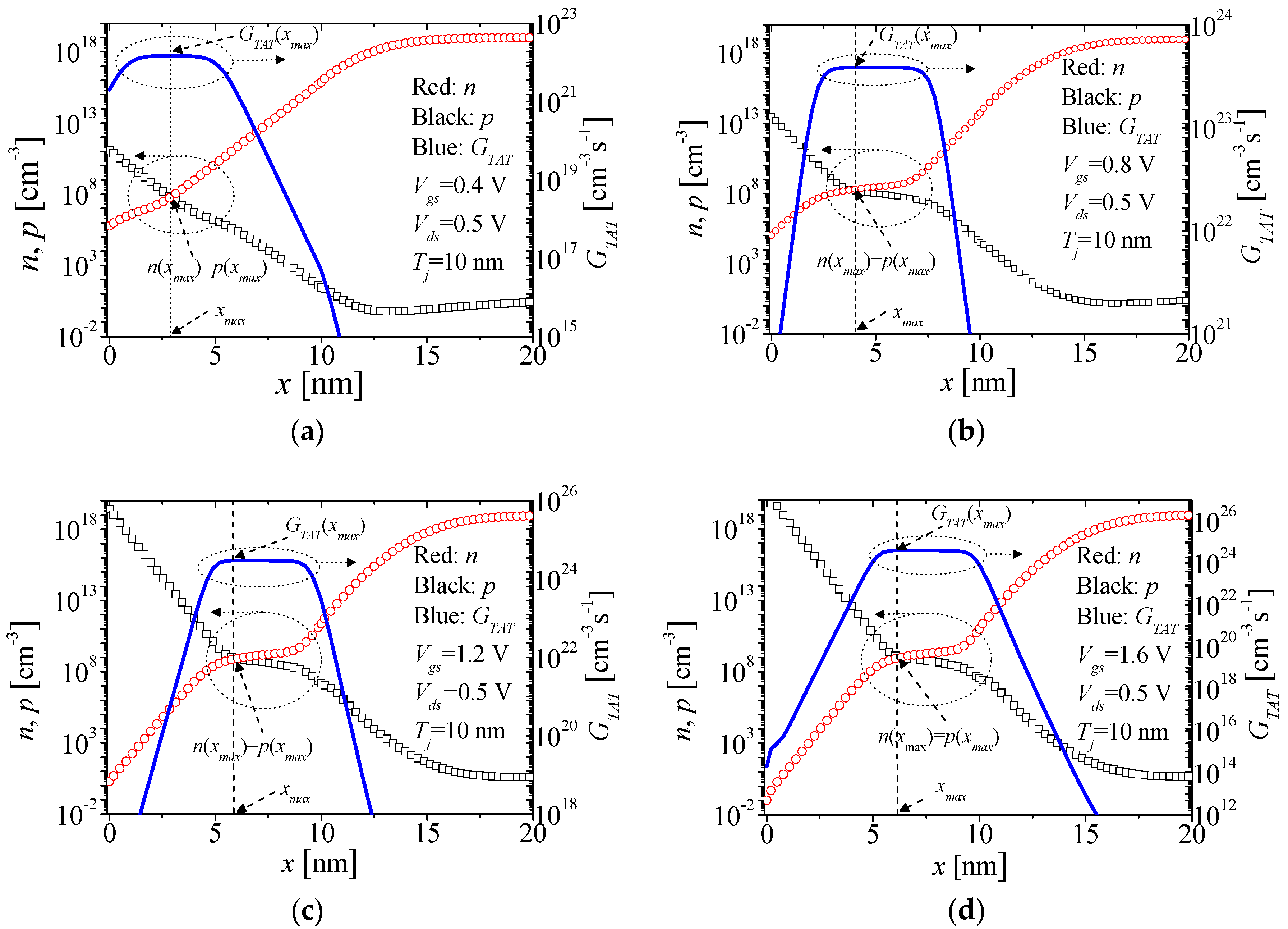
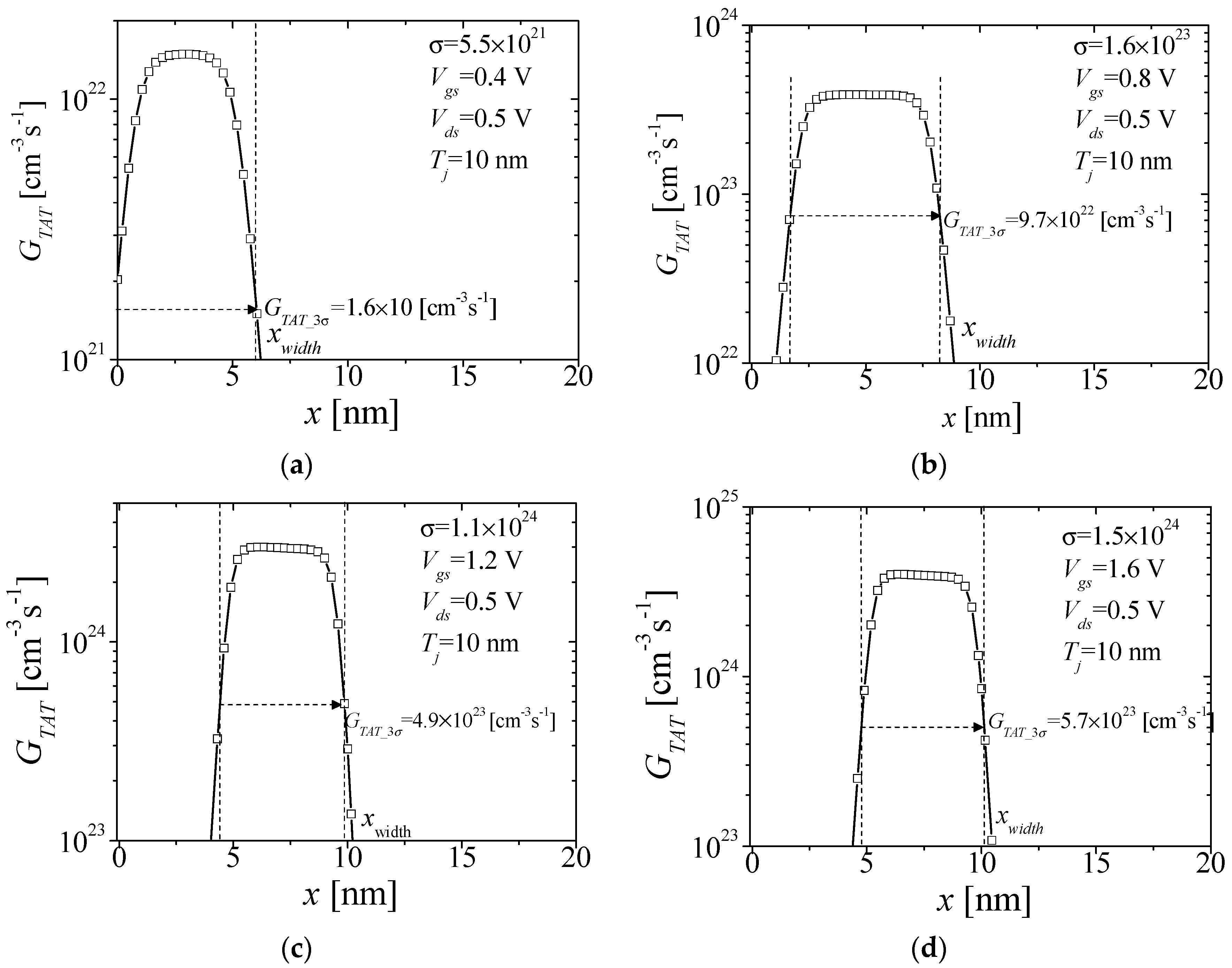
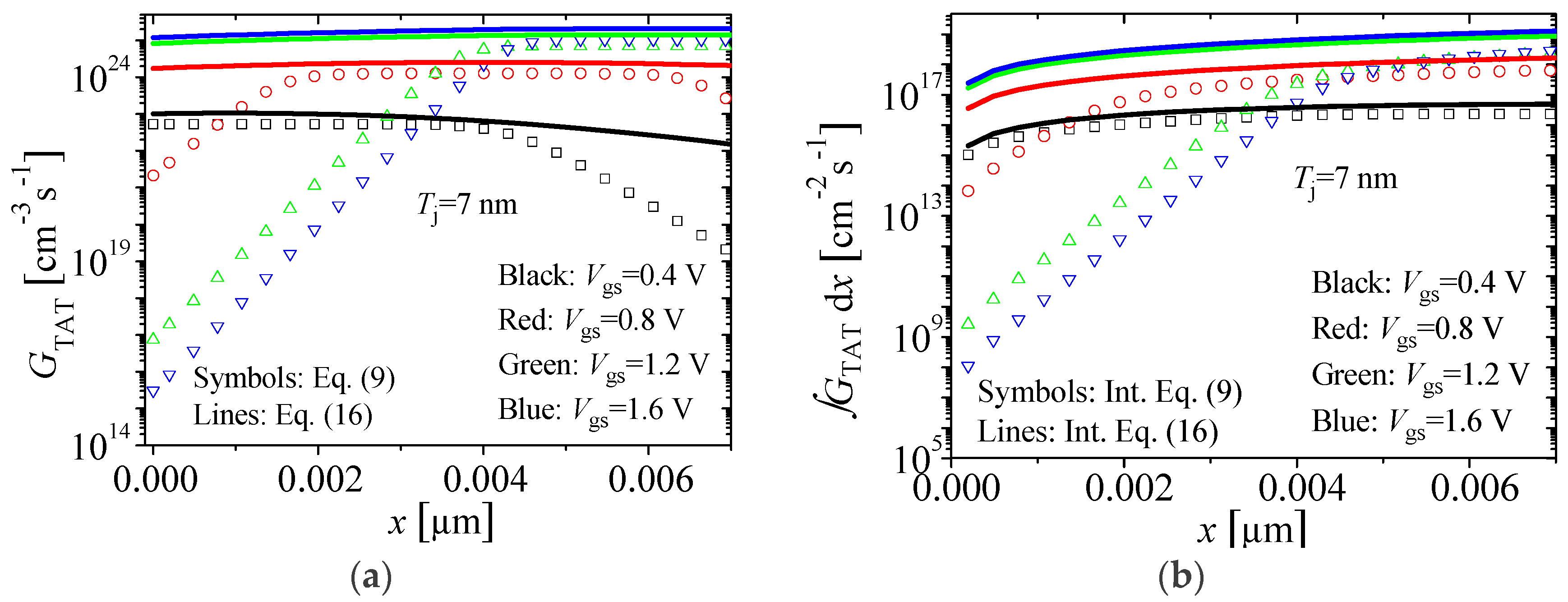

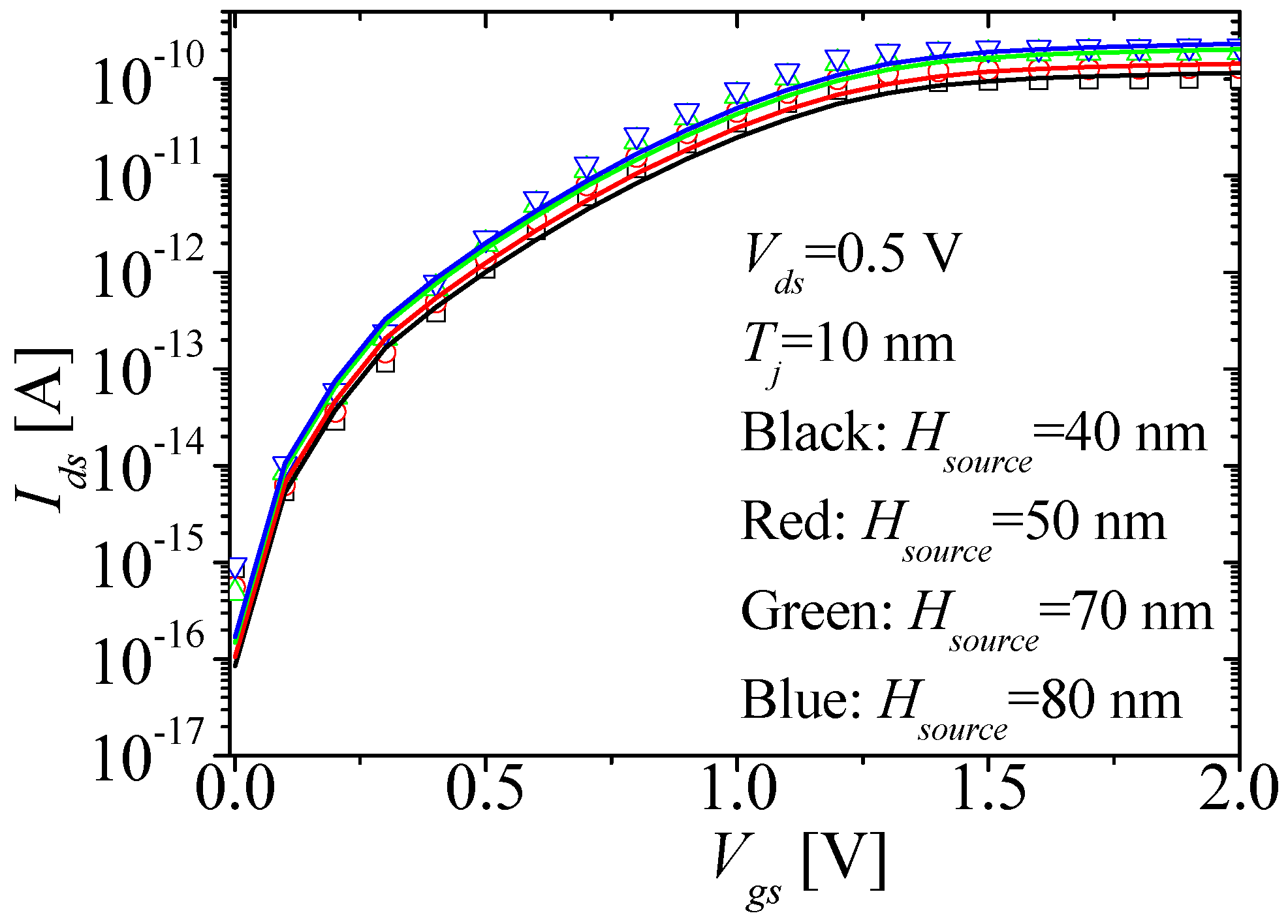
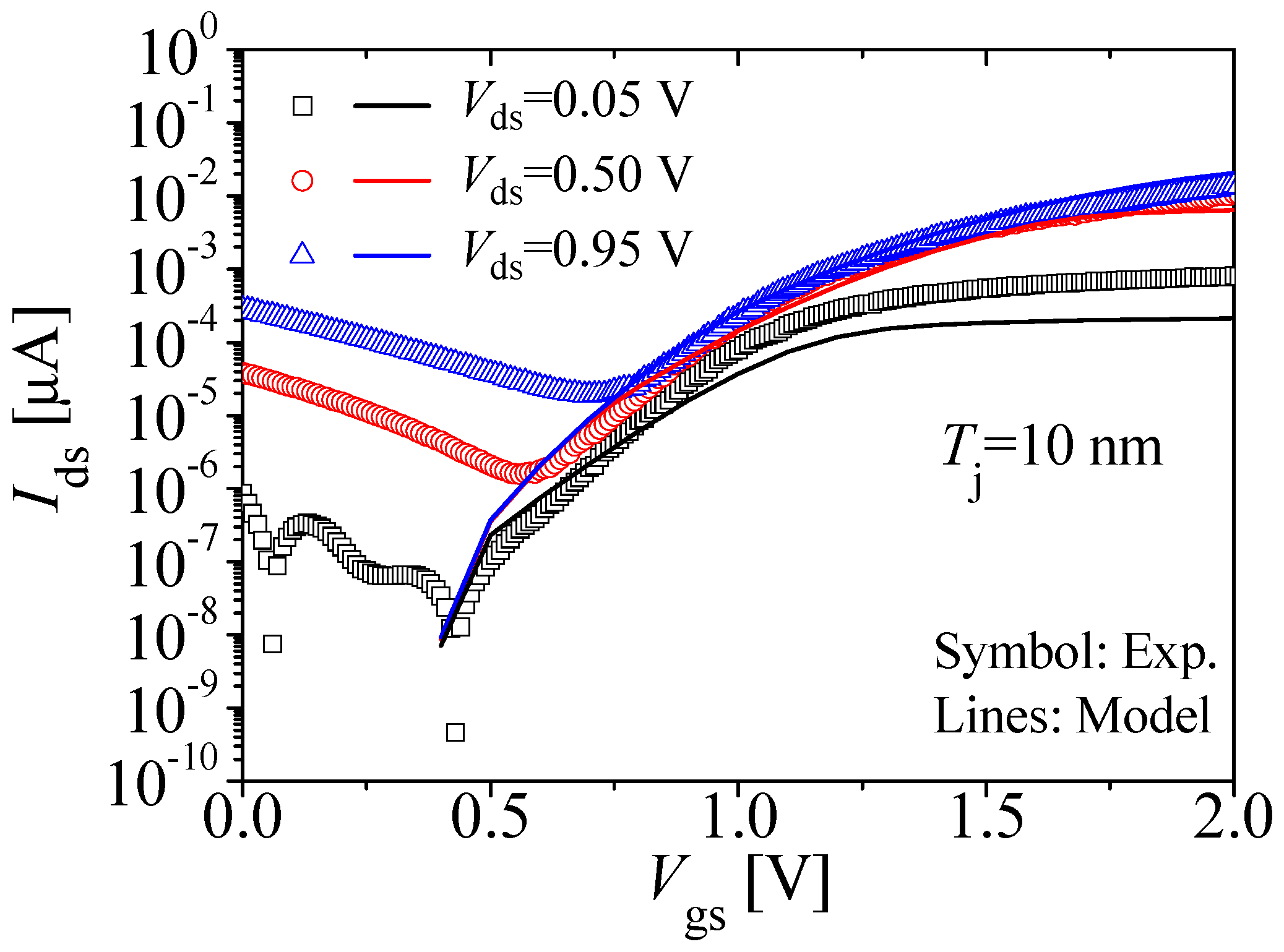
| Mechanism | Region Dominated | Threshold Voltage |
|---|---|---|
| 2D BTBT | Typically intermediate bias region. | TAT < 2D BTBT < 1D BTBT |
| 1D BTBT | Typically subthreshold region. | |
| TAT | Typically subthreshold and intermediate bias regions [5], and in extreme cases [13] the high bias region as well. |
| Symbol | Description | Value/Unit |
|---|---|---|
| φsource | Potential at source edge | V |
| Na, Nd | Source, channel doping | cm−3 |
| xsource, xchannel | x co-ordinate in source, channel | cm |
| Ldep | Depletion length in source | cm |
| εsi, εox | Silicon, oxide permittivity | 11.9Ɛ0, 25Ɛ0 |
| Vfb, | Flat band voltage | V |
| q | Electron charge | 1.6 × 10−19 C |
| φs,φj,φchannel | Surface potential at xchannel = 0, junction potential at x = Tj, and potential as a function of xchannel, respectively | V |
| φ;dep | Depletion potential in source | V |
| Cox | Gate capacitance | F/cm2 |
| Vbis | Channel/source junction built-in potential | V |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Najam, F.; Yu, Y.S. Compact Trap-Assisted-Tunneling Model for Line Tunneling Field-Effect-Transistor Devices. Appl. Sci. 2020, 10, 4475. https://doi.org/10.3390/app10134475
Najam F, Yu YS. Compact Trap-Assisted-Tunneling Model for Line Tunneling Field-Effect-Transistor Devices. Applied Sciences. 2020; 10(13):4475. https://doi.org/10.3390/app10134475
Chicago/Turabian StyleNajam, Faraz, and Yun Seop Yu. 2020. "Compact Trap-Assisted-Tunneling Model for Line Tunneling Field-Effect-Transistor Devices" Applied Sciences 10, no. 13: 4475. https://doi.org/10.3390/app10134475
APA StyleNajam, F., & Yu, Y. S. (2020). Compact Trap-Assisted-Tunneling Model for Line Tunneling Field-Effect-Transistor Devices. Applied Sciences, 10(13), 4475. https://doi.org/10.3390/app10134475






